Active Learning for Hidden Attributes in Networks
Paper and Code
May 05, 2010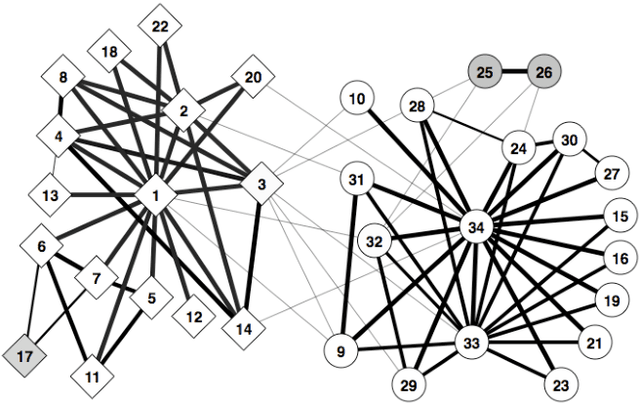
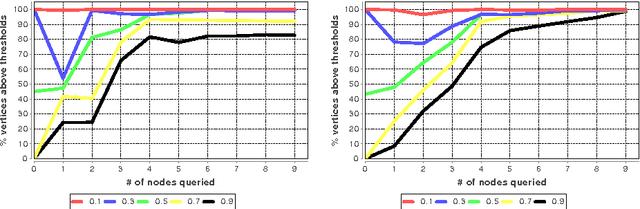
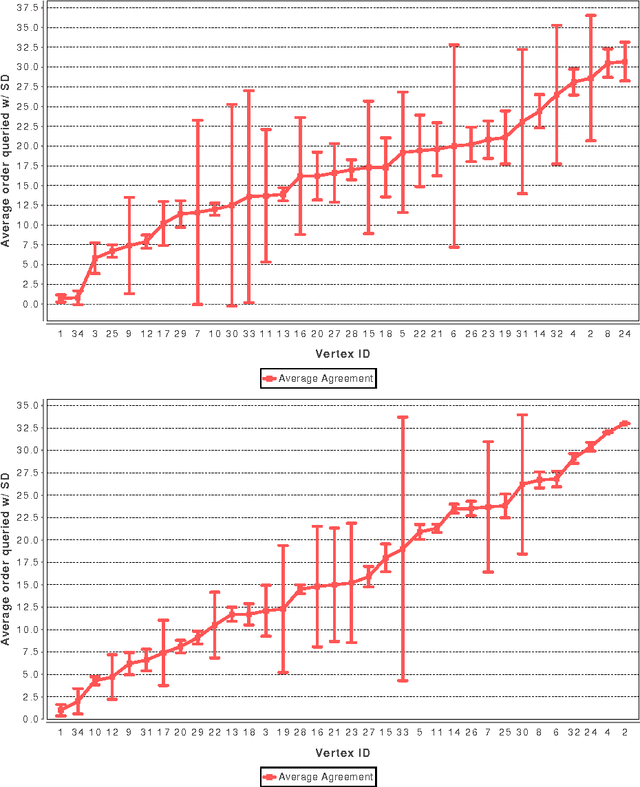
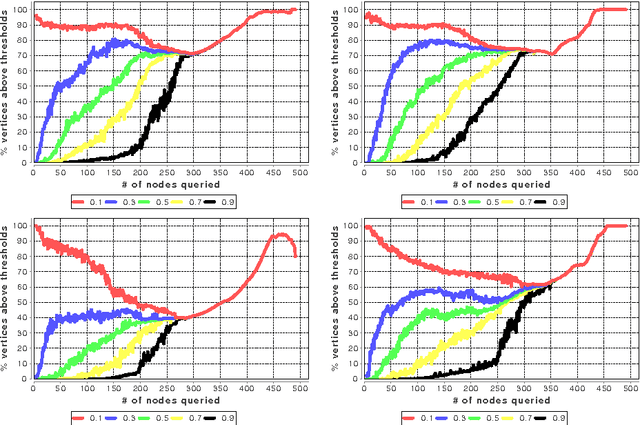
In many networks, vertices have hidden attributes, or types, that are correlated with the networks topology. If the topology is known but these attributes are not, and if learning the attributes is costly, we need a method for choosing which vertex to query in order to learn as much as possible about the attributes of the other vertices. We assume the network is generated by a stochastic block model, but we make no assumptions about its assortativity or disassortativity. We choose which vertex to query using two methods: 1) maximizing the mutual information between its attributes and those of the others (a well-known approach in active learning) and 2) maximizing the average agreement between two independent samples of the conditional Gibbs distribution. Experimental results show that both these methods do much better than simple heuristics. They also consistently identify certain vertices as important by querying them early on.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge