Smoothness and Structure Learning by Proxy
Paper and Code
Jun 27, 2012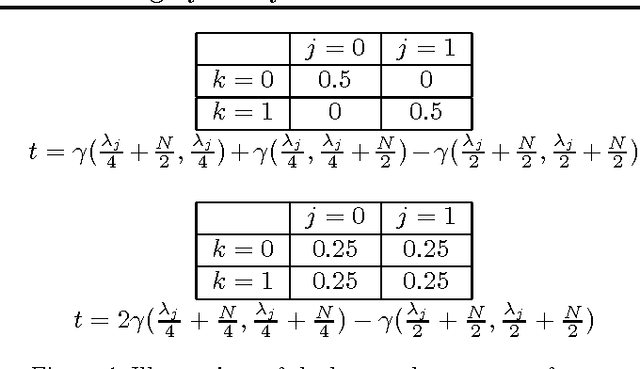
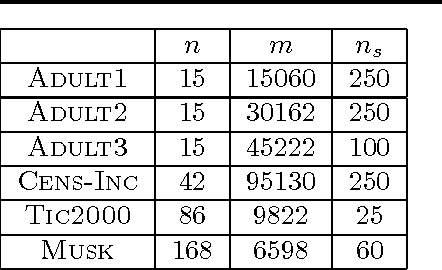
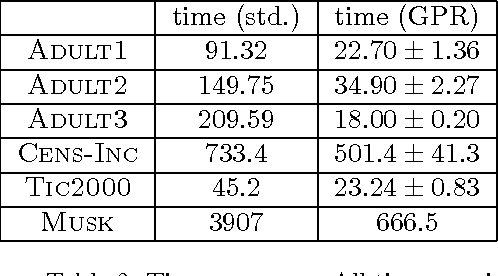
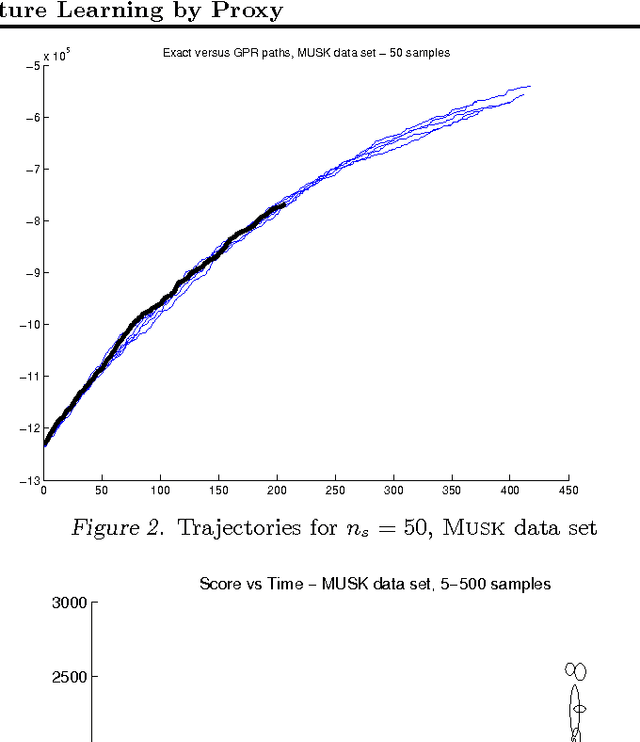
As data sets grow in size, the ability of learning methods to find structure in them is increasingly hampered by the time needed to search the large spaces of possibilities and generate a score for each that takes all of the observed data into account. For instance, Bayesian networks, the model chosen in this paper, have a super-exponentially large search space for a fixed number of variables. One possible method to alleviate this problem is to use a proxy, such as a Gaussian Process regressor, in place of the true scoring function, training it on a selection of sampled networks. We prove here that the use of such a proxy is well-founded, as we can bound the smoothness of a commonly-used scoring function for Bayesian network structure learning. We show here that, compared to an identical search strategy using the network?s exact scores, our proxy-based search is able to get equivalent or better scores on a number of data sets in a fraction of the time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge