Oriented and Degree-generated Block Models: Generating and Inferring Communities with Inhomogeneous Degree Distributions
Paper and Code
May 31, 2012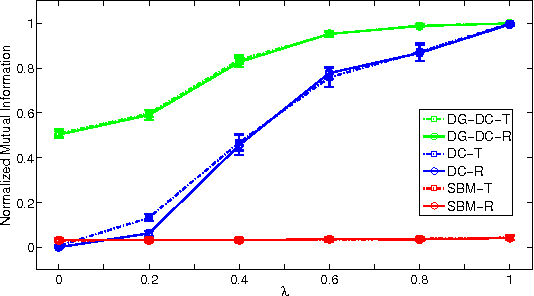
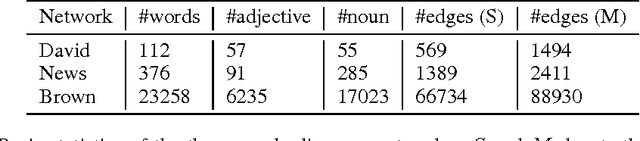

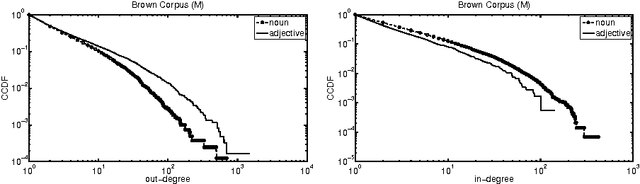
The stochastic block model is a powerful tool for inferring community structure from network topology. However, it predicts a Poisson degree distribution within each community, while most real-world networks have a heavy-tailed degree distribution. The degree-corrected block model can accommodate arbitrary degree distributions within communities. But since it takes the vertex degrees as parameters rather than generating them, it cannot use them to help it classify the vertices, and its natural generalization to directed graphs cannot even use the orientations of the edges. In this paper, we present variants of the block model with the best of both worlds: they can use vertex degrees and edge orientations in the classification process, while tolerating heavy-tailed degree distributions within communities. We show that for some networks, including synthetic networks and networks of word adjacencies in English text, these new block models achieve a higher accuracy than either standard or degree-corrected block models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge