The Joint Weighted Average (JWA) Operator

Information aggregation is a vital tool for human and machine decision making, especially in the presence of noise and uncertainty. Traditionally, approaches to aggregation broadly diverge into two categories, those which attribute a worth or weight to information sources and those which attribute said worth to the evidence arising from said sources. The latter is pervasive in particular in the physical sciences, underpinning linear order statistics and enabling non-linear aggregation. The former is popular in the social sciences, providing interpretable insight on the sources. Thus far, limited work has sought to integrate both approaches, applying either approach to a different degree. In this paper, we put forward an approach which integrates--rather than partially applies--both approaches, resulting in a novel joint weighted averaging operator. We show how this operator provides a systematic approach to integrating a priori beliefs about the worth of both source and evidence by leveraging compositional geometry--producing results unachievable by traditional operators. We conclude and highlight the potential of the operator across disciplines, from machine learning to psychology.

Characterizing the robustness of Bayesian adaptive experimental designs to active learning bias

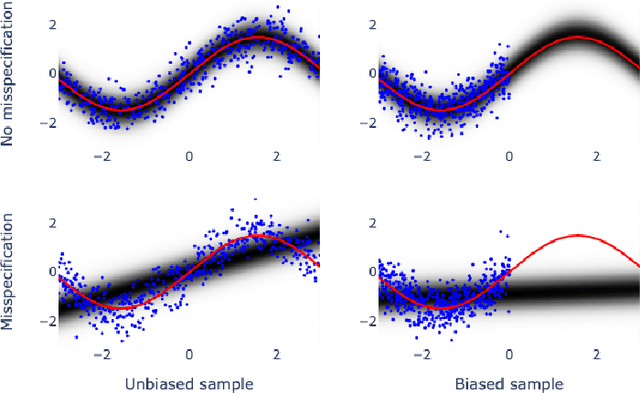
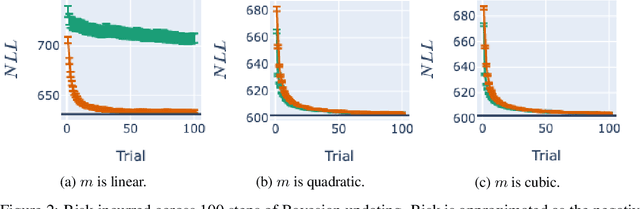
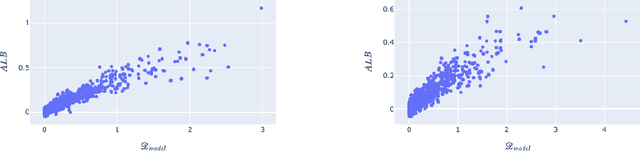
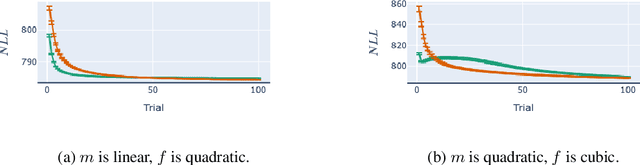
Bayesian adaptive experimental design is a form of active learning, which chooses samples to maximize the information they give about uncertain parameters. Prior work has shown that other forms of active learning can suffer from active learning bias, where unrepresentative sampling leads to inconsistent parameter estimates. We show that active learning bias can also afflict Bayesian adaptive experimental design, depending on model misspecification. We develop an information-theoretic measure of misspecification, and show that worse misspecification implies more severe active learning bias. At the same time, model classes incorporating more "noise" - i.e., specifying higher inherent variance in observations - suffer less from active learning bias, because their predictive distributions are likely to overlap more with the true distribution. Finally, we show how these insights apply to a (simulated) preference learning experiment.