Memory-Based Dual Gaussian Processes for Sequential Learning

Sequential learning with Gaussian processes (GPs) is challenging when access to past data is limited, for example, in continual and active learning. In such cases, errors can accumulate over time due to inaccuracies in the posterior, hyperparameters, and inducing points, making accurate learning challenging. Here, we present a method to keep all such errors in check using the recently proposed dual sparse variational GP. Our method enables accurate inference for generic likelihoods and improves learning by actively building and updating a memory of past data. We demonstrate its effectiveness in several applications involving Bayesian optimization, active learning, and continual learning.

Cost-aware learning of relevant contextual variables within Bayesian optimization

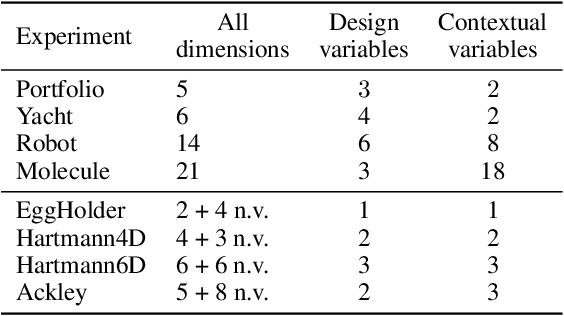
Contextual Bayesian Optimization (CBO) is a powerful framework for optimizing black-box, expensive-to-evaluate functions with respect to design variables, while simultaneously efficiently integrating relevant contextual information regarding the environment, such as experimental conditions. However, in many practical scenarios, the relevance of contextual variables is not necessarily known beforehand. Moreover, the contextual variables can sometimes be optimized themselves, a setting that current CBO algorithms do not take into account. Optimizing contextual variables may be costly, which raises the question of determining a minimal relevant subset. In this paper, we frame this problem as a cost-aware model selection BO task and address it using a novel method, Sensitivity-Analysis-Driven Contextual BO (SADCBO). We learn the relevance of context variables by sensitivity analysis of the posterior surrogate model at specific input points, whilst minimizing the cost of optimization by leveraging recent developments on early stopping for BO. We empirically evaluate our proposed SADCBO against alternatives on synthetic experiments together with extensive ablation studies, and demonstrate a consistent improvement across examples.

Large-Scale Cox Process Inference using Variational Fourier Features

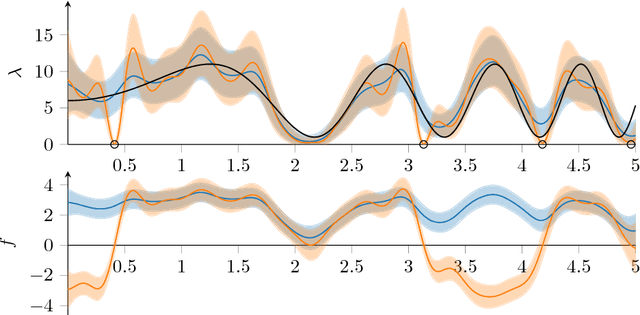
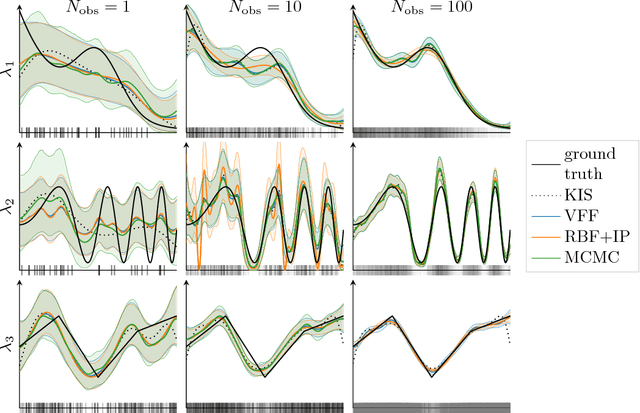
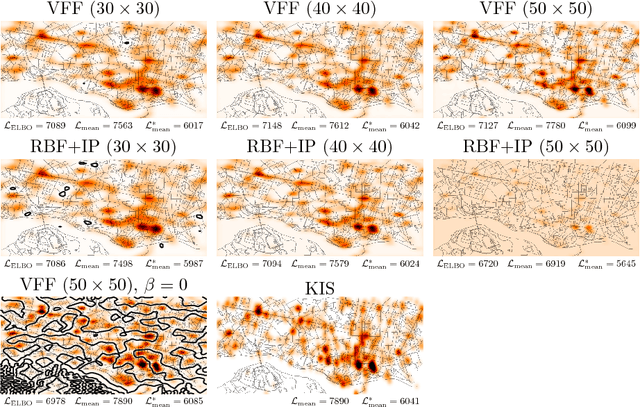
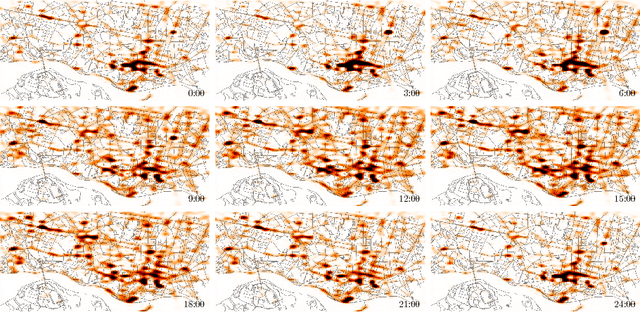
Gaussian process modulated Poisson processes provide a flexible framework for modelling spatiotemporal point patterns. So far this had been restricted to one dimension, binning to a pre-determined grid, or small data sets of up to a few thousand data points. Here we introduce Cox process inference based on Fourier features. This sparse representation induces global rather than local constraints on the function space and is computationally efficient. This allows us to formulate a grid-free approximation that scales well with the number of data points and the size of the domain. We demonstrate that this allows MCMC approximations to the non-Gaussian posterior. We also find that, in practice, Fourier features have more consistent optimization behavior than previous approaches. Our approximate Bayesian method can fit over 100,000 events with complex spatiotemporal patterns in three dimensions on a single GPU.