Likelihood-free Model Choice for Simulator-based Models with the Jensen--Shannon Divergence

Choice of appropriate structure and parametric dimension of a model in the light of data has a rich history in statistical research, where the first seminal approaches were developed in 1970s, such as the Akaike's and Schwarz's model scoring criteria that were inspired by information theory and embodied the rationale called Occam's razor. After those pioneering works, model choice was quickly established as its own field of research, gaining considerable attention in both computer science and statistics. However, to date, there have been limited attempts to derive scoring criteria for simulator-based models lacking a likelihood expression. Bayes factors have been considered for such models, but arguments have been put both for and against use of them and around issues related to their consistency. Here we use the asymptotic properties of Jensen--Shannon divergence (JSD) to derive a consistent model scoring criterion for the likelihood-free setting called JSD-Razor. Relationships of JSD-Razor with established scoring criteria for the likelihood-based approach are analyzed and we demonstrate the favorable properties of our criterion using both synthetic and real modeling examples.

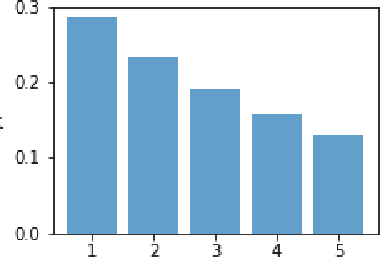
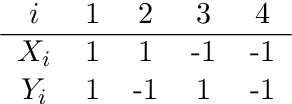
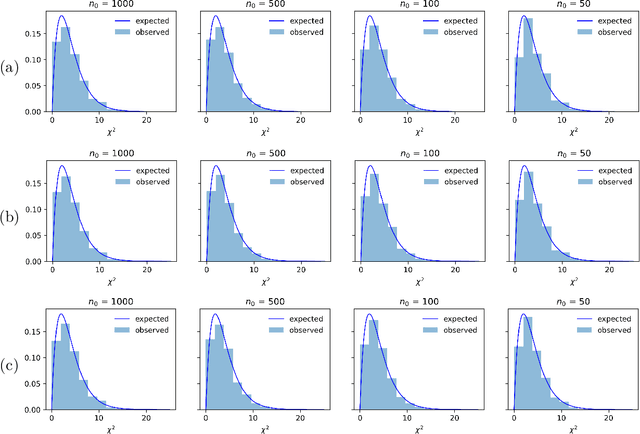
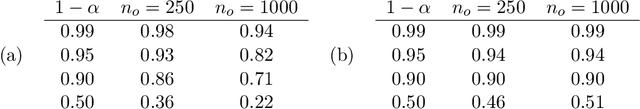
Nonparametric likelihood-free inference with Jensen-Shannon divergence for simulator-based models with categorical output

Likelihood-free inference for simulator-based statistical models has recently attracted a surge of interest, both in the machine learning and statistics communities. The primary focus of these research fields has been to approximate the posterior distribution of model parameters, either by various types of Monte Carlo sampling algorithms or deep neural network -based surrogate models. Frequentist inference for simulator-based models has been given much less attention to date, despite that it would be particularly amenable to applications with big data where implicit asymptotic approximation of the likelihood is expected to be accurate and can leverage computationally efficient strategies. Here we derive a set of theoretical results to enable estimation, hypothesis testing and construction of confidence intervals for model parameters using asymptotic properties of the Jensen--Shannon divergence. Such asymptotic approximation offers a rapid alternative to more computation-intensive approaches and can be attractive for diverse applications of simulator-based models. 61

Testing for Causality in Continuous Time Bayesian Network Models of High-Frequency Data

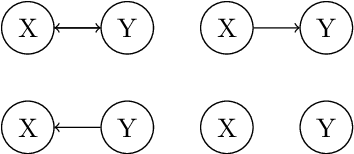
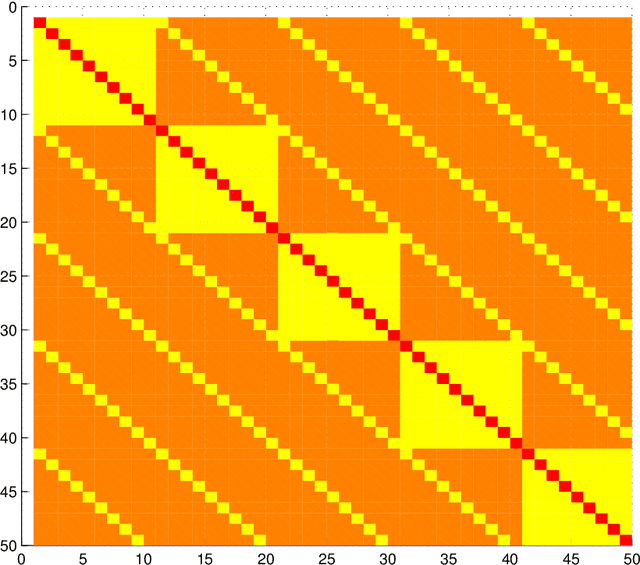
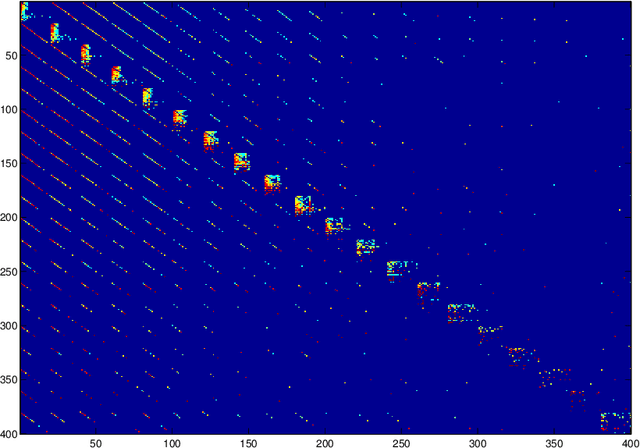
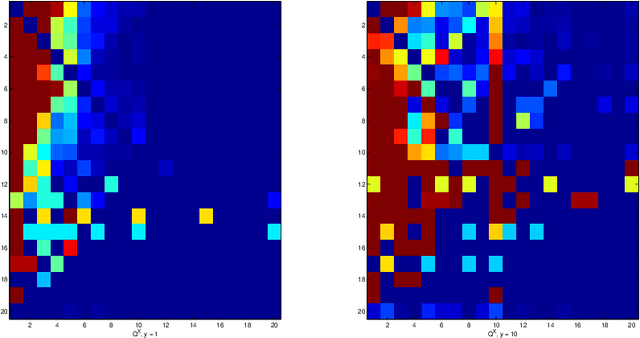
Continuous time Bayesian networks are investigated with a special focus on their ability to express causality. A framework is presented for doing inference in these networks. The central contributions are a representation of the intensity matrices for the networks and the introduction of a causality measure. A new model for high-frequency financial data is presented. It is calibrated to market data and by the new causality measure it performs better than older models.

Context-specific independence in graphical log-linear models

Log-linear models are the popular workhorses of analyzing contingency tables. A log-linear parameterization of an interaction model can be more expressive than a direct parameterization based on probabilities, leading to a powerful way of defining restrictions derived from marginal, conditional and context-specific independence. However, parameter estimation is often simpler under a direct parameterization, provided that the model enjoys certain decomposability properties. Here we introduce a cyclical projection algorithm for obtaining maximum likelihood estimates of log-linear parameters under an arbitrary context-specific graphical log-linear model, which needs not satisfy criteria of decomposability. We illustrate that lifting the restriction of decomposability makes the models more expressive, such that additional context-specific independencies embedded in real data can be identified. It is also shown how a context-specific graphical model can correspond to a non-hierarchical log-linear parameterization with a concise interpretation. This observation can pave way to further development of non-hierarchical log-linear models, which have been largely neglected due to their believed lack of interpretability.

Stratified Graphical Models - Context-Specific Independence in Graphical Models

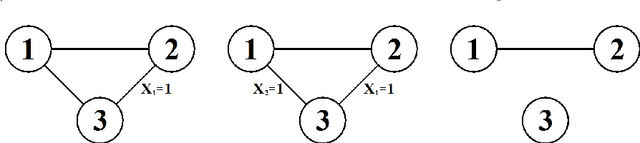
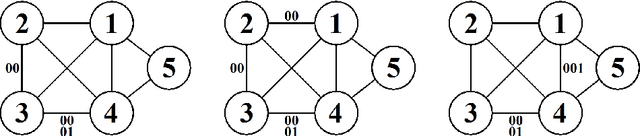
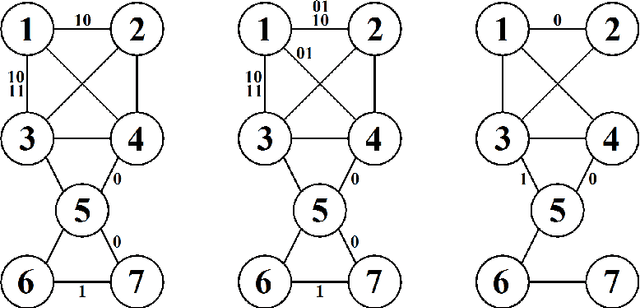
Theory of graphical models has matured over more than three decades to provide the backbone for several classes of models that are used in a myriad of applications such as genetic mapping of diseases, credit risk evaluation, reliability and computer security, etc. Despite of their generic applicability and wide adoptance, the constraints imposed by undirected graphical models and Bayesian networks have also been recognized to be unnecessarily stringent under certain circumstances. This observation has led to the proposal of several generalizations that aim at more relaxed constraints by which the models can impose local or context-specific dependence structures. Here we consider an additional class of such models, termed as stratified graphical models. We develop a method for Bayesian learning of these models by deriving an analytical expression for the marginal likelihood of data under a specific subclass of decomposable stratified models. A non-reversible Markov chain Monte Carlo approach is further used to identify models that are highly supported by the posterior distribution over the model space. Our method is illustrated and compared with ordinary graphical models through application to several real and synthetic datasets.

Labeled Directed Acyclic Graphs: a generalization of context-specific independence in directed graphical models

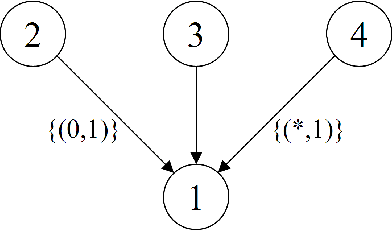
We introduce a novel class of labeled directed acyclic graph (LDAG) models for finite sets of discrete variables. LDAGs generalize earlier proposals for allowing local structures in the conditional probability distribution of a node, such that unrestricted label sets determine which edges can be deleted from the underlying directed acyclic graph (DAG) for a given context. Several properties of these models are derived, including a generalization of the concept of Markov equivalence classes. Efficient Bayesian learning of LDAGs is enabled by introducing an LDAG-based factorization of the Dirichlet prior for the model parameters, such that the marginal likelihood can be calculated analytically. In addition, we develop a novel prior distribution for the model structures that can appropriately penalize a model for its labeling complexity. A non-reversible Markov chain Monte Carlo algorithm combined with a greedy hill climbing approach is used for illustrating the useful properties of LDAG models for both real and synthetic data sets.