Globally Interpretable Classifiers via Boolean Formulas with Dynamic Propositions

Interpretability and explainability are among the most important challenges of modern artificial intelligence, being mentioned even in various legislative sources. In this article, we develop a method for extracting immediately human interpretable classifiers from tabular data. The classifiers are given in the form of short Boolean formulas built with propositions that can either be directly extracted from categorical attributes or dynamically computed from numeric ones. Our method is implemented using Answer Set Programming. We investigate seven datasets and compare our results to ones obtainable by state-of-the-art classifiers for tabular data, namely, XGBoost and random forests. Over all datasets, the accuracies obtainable by our method are similar to the reference methods. The advantage of our classifiers in all cases is that they are very short and immediately human intelligible as opposed to the black-box nature of the reference methods.

Interpretable classifiers for tabular data via discretization and feature selection

We introduce a method for computing immediately human interpretable yet accurate classifiers from tabular data. The classifiers obtained are short DNF-formulas, computed via first discretizing the original data to Boolean form and then using feature selection coupled with a very fast algorithm for producing the best possible Boolean classifier for the setting. We demonstrate the approach via 14 experiments, obtaining results with accuracies mainly similar to ones obtained via random forests, XGBoost, and existing results for the same datasets in the literature. In several cases, our approach in fact outperforms the reference results in relation to accuracy, even though the main objective of our study is the immediate interpretability of our classifiers. We also prove a new result on the probability that the classifier we obtain from real-life data corresponds to the ideally best classifier with respect to the background distribution the data comes from.

Generalizing Level Ranking Constraints for Monotone and Convex Aggregates

In answer set programming (ASP), answer sets capture solutions to search problems of interest and thus the efficient computation of answer sets is of utmost importance. One viable implementation strategy is provided by translation-based ASP where logic programs are translated into other KR formalisms such as Boolean satisfiability (SAT), SAT modulo theories (SMT), and mixed-integer programming (MIP). Consequently, existing solvers can be harnessed for the computation of answer sets. Many of the existing translations rely on program completion and level rankings to capture the minimality of answer sets and default negation properly. In this work, we take level ranking constraints into reconsideration, aiming at their generalizations to cover aggregate-based extensions of ASP in more systematic way. By applying a number of program transformations, ranking constraints can be rewritten in a general form that preserves the structure of monotone and convex aggregates and thus offers a uniform basis for their incorporation into translation-based ASP. The results open up new possibilities for the implementation of translators and solver pipelines in practice.

Short Boolean Formulas as Explanations in Practice

We investigate explainability via short Boolean formulas in the data model based on unary relations. As an explanation of length k, we take a Boolean formula of length k that minimizes the error with respect to the target attribute to be explained. We first provide novel quantitative bounds for the expected error in this scenario. We then also demonstrate how the setting works in practice by studying three concrete data sets. In each case, we calculate explanation formulas of different lengths using an encoding in Answer Set Programming. The most accurate formulas we obtain achieve errors similar to other methods on the same data sets. However, due to overfitting, these formulas are not necessarily ideal explanations, so we use cross validation to identify a suitable length for explanations. By limiting to shorter formulas, we obtain explanations that avoid overfitting but are still reasonably accurate and also, importantly, human interpretable.

Capturing (Optimal) Relaxed Plans with Stable and Supported Models of Logic Programs

We establish a novel relation between delete-free planning, an important task for the AI Planning community also known as relaxed planning, and logic programming. We show that given a planning problem, all subsets of actions that could be ordered to produce relaxed plans for the problem can be bijectively captured with stable models of a logic program describing the corresponding relaxed planning problem. We also consider the supported model semantics of logic programs, and introduce one causal and one diagnostic encoding of the relaxed planning problem as logic programs, both capturing relaxed plans with their supported models. Our experimental results show that these new encodings can provide major performance gain when computing optimal relaxed plans, with our diagnostic encoding outperforming state-of-the-art approaches to relaxed planning regardless of the given time limit when measured on a wide collection of STRIPS planning benchmarks.

Explainability via Short Formulas: the Case of Propositional Logic with Implementation

We conceptualize explainability in terms of logic and formula size, giving a number of related definitions of explainability in a very general setting. Our main interest is the so-called special explanation problem which aims to explain the truth value of an input formula in an input model. The explanation is a formula of minimal size that (1) agrees with the input formula on the input model and (2) transmits the involved truth value to the input formula globally, i.e., on every model. As an important example case, we study propositional logic in this setting and show that the special explainability problem is complete for the second level of the polynomial hierarchy. We also provide an implementation of this problem in answer set programming and investigate its capacity in relation to explaining answers to the n-queens and dominating set problems.

plingo: A system for probabilistic reasoning in clingo based on lpmln

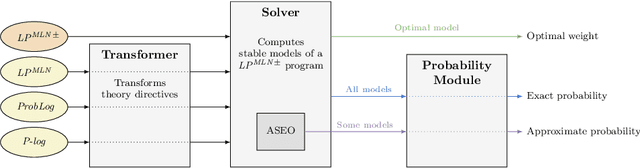
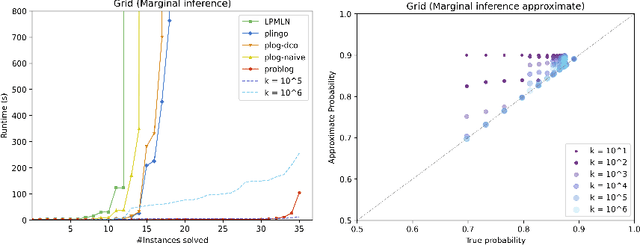
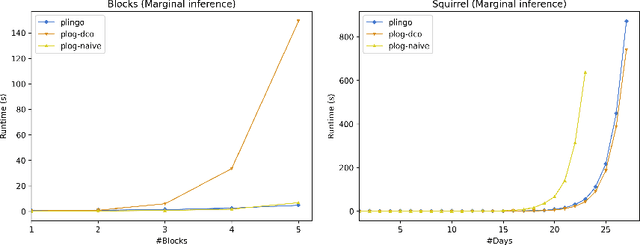
We present plingo, an extension of the ASP system clingo with various probabilistic reasoning modes. Plingo is centered upon LP^MLN, a probabilistic extension of ASP based on a weight scheme from Markov Logic. This choice is motivated by the fact that the core probabilistic reasoning modes can be mapped onto optimization problems and that LP^MLN may serve as a middle-ground formalism connecting to other probabilistic approaches. As a result, plingo offers three alternative frontends, for LP^MLN, P-log, and ProbLog. The corresponding input languages and reasoning modes are implemented by means of clingo's multi-shot and theory solving capabilities. The core of plingo amounts to a re-implementation of LP^MLN in terms of modern ASP technology, extended by an approximation technique based on a new method for answer set enumeration in the order of optimality. We evaluate plingo's performance empirically by comparing it to other probabilistic systems.

Solution Enumeration by Optimality in Answer Set Programming

Given a combinatorial search problem, it may be highly useful to enumerate its (all) solutions besides just finding one solution, or showing that none exists. The same can be stated about optimal solutions if an objective function is provided. This work goes beyond the bare enumeration of optimal solutions and addresses the computational task of solution enumeration by optimality (SEO). This task is studied in the context of Answer Set Programming (ASP) where (optimal) solutions of a problem are captured with the answer sets of a logic program encoding the problem. Existing answer-set solvers already support the enumeration of all (optimal) answer sets. However, in this work, we generalize the enumeration of optimal answer sets beyond strictly optimal ones, giving rise to the idea of answer set enumeration in the order of optimality (ASEO). This approach is applicable up to the best k answer sets or in an unlimited setting, which amounts to a process of sorting answer sets based on the objective function. As the main contribution of this work, we present the first general algorithms for the aforementioned tasks of answer set enumeration. Moreover, we illustrate the potential use cases of ASEO. First, we study how efficiently access to the next-best solutions can be achieved in a number of optimization problems that have been formalized and solved in ASP. Second, we show that ASEO provides us with an effective sampling technique for Bayesian networks.

Allen's Interval Algebra Makes the Difference

Allen's Interval Algebra constitutes a framework for reasoning about temporal information in a qualitative manner. In particular, it uses intervals, i.e., pairs of endpoints, on the timeline to represent entities corresponding to actions, events, or tasks, and binary relations such as precedes and overlaps to encode the possible configurations between those entities. Allen's calculus has found its way in many academic and industrial applications that involve, most commonly, planning and scheduling, temporal databases, and healthcare. In this paper, we present a novel encoding of Interval Algebra using answer-set programming (ASP) extended by difference constraints, i.e., the fragment abbreviated as ASP(DL), and demonstrate its performance via a preliminary experimental evaluation. Although our ASP encoding is presented in the case of Allen's calculus for the sake of clarity, we suggest that analogous encodings can be devised for other point-based calculi, too.

Clingo goes Linear Constraints over Reals and Integers

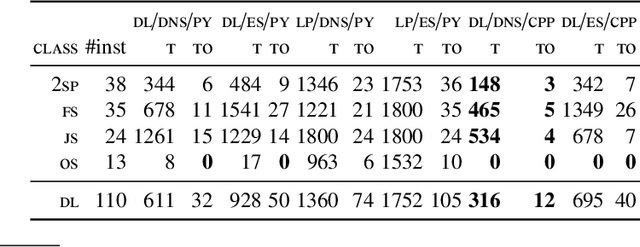
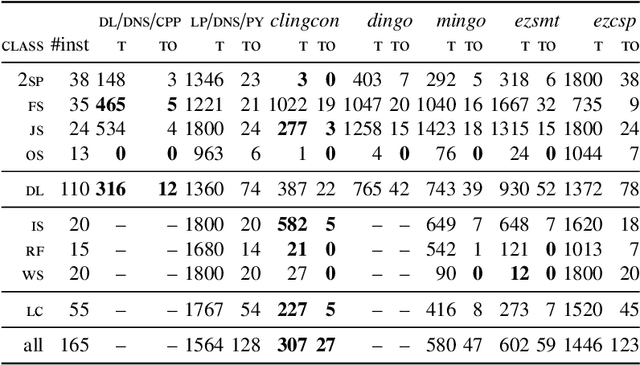
The recent series 5 of the ASP system clingo provides generic means to enhance basic Answer Set Programming (ASP) with theory reasoning capabilities. We instantiate this framework with different forms of linear constraints, discuss the respective implementations, and present techniques of how to use these constraints in a reactive context. More precisely, we introduce extensions to clingo with difference and linear constraints over integers and reals, respectively, and realize them in complementary ways. Finally, we empirically evaluate the resulting clingo derivatives clingo[dl] and clingo[lp] on common fragments and contrast them to related ASP systems. This paper is under consideration for acceptance in TPLP.