Neuro-Symbolic Spatio-Temporal Reasoning

Knowledge about space and time is necessary to solve problems in the physical world: An AI agent situated in the physical world and interacting with objects often needs to reason about positions of and relations between objects; and as soon as the agent plans its actions to solve a task, it needs to consider the temporal aspect (e.g., what actions to perform over time). Spatio-temporal knowledge, however, is required beyond interacting with the physical world, and is also often transferred to the abstract world of concepts through analogies and metaphors (e.g., "a threat that is hanging over our heads"). As spatial and temporal reasoning is ubiquitous, different attempts have been made to integrate this into AI systems. In the area of knowledge representation, spatial and temporal reasoning has been largely limited to modeling objects and relations and developing reasoning methods to verify statements about objects and relations. On the other hand, neural network researchers have tried to teach models to learn spatial relations from data with limited reasoning capabilities. Bridging the gap between these two approaches in a mutually beneficial way could allow us to tackle many complex real-world problems, such as natural language processing, visual question answering, and semantic image segmentation. In this chapter, we view this integration problem from the perspective of Neuro-Symbolic AI. Specifically, we propose a synergy between logical reasoning and machine learning that will be grounded on spatial and temporal knowledge. Describing some successful applications, remaining challenges, and evaluation datasets pertaining to this direction is the main topic of this contribution.

Allen's Interval Algebra Makes the Difference

Allen's Interval Algebra constitutes a framework for reasoning about temporal information in a qualitative manner. In particular, it uses intervals, i.e., pairs of endpoints, on the timeline to represent entities corresponding to actions, events, or tasks, and binary relations such as precedes and overlaps to encode the possible configurations between those entities. Allen's calculus has found its way in many academic and industrial applications that involve, most commonly, planning and scheduling, temporal databases, and healthcare. In this paper, we present a novel encoding of Interval Algebra using answer-set programming (ASP) extended by difference constraints, i.e., the fragment abbreviated as ASP(DL), and demonstrate its performance via a preliminary experimental evaluation. Although our ASP encoding is presented in the case of Allen's calculus for the sake of clarity, we suggest that analogous encodings can be devised for other point-based calculi, too.

Semantic Referee: A Neural-Symbolic Framework for Enhancing Geospatial Semantic Segmentation

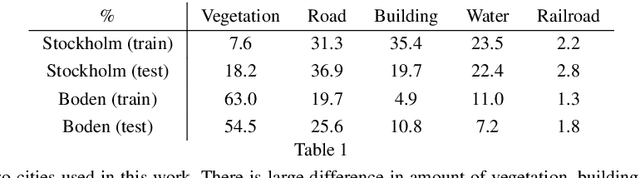
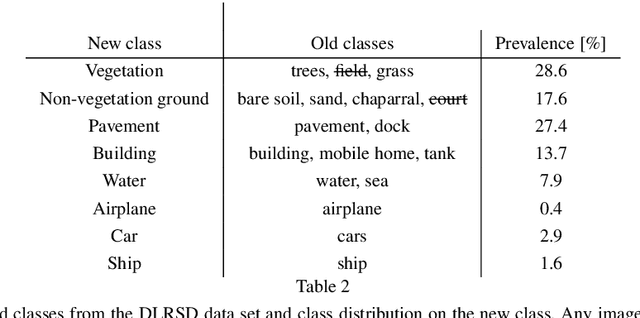
Understanding why machine learning algorithms may fail is usually the task of the human expert that uses domain knowledge and contextual information to discover systematic shortcomings in either the data or the algorithm. In this paper, we propose a semantic referee, which is able to extract qualitative features of the errors emerging from deep machine learning frameworks and suggest corrections. The semantic referee relies on ontological reasoning about spatial knowledge in order to characterize errors in terms of their spatial relations with the environment. Using semantics, the reasoner interacts with the learning algorithm as a supervisor. In this paper, the proposed method of the interaction between a neural network classifier and a semantic referee shows how to improve the performance of semantic segmentation for satellite imagery data.

Exploring Directional Path-Consistency for Solving Constraint Networks

Among the local consistency techniques used for solving constraint networks, path-consistency (PC) has received a great deal of attention. However, enforcing PC is computationally expensive and sometimes even unnecessary. Directional path-consistency (DPC) is a weaker notion of PC that considers a given variable ordering and can thus be enforced more efficiently than PC. This paper shows that DPC (the DPC enforcing algorithm of Dechter and Pearl) decides the constraint satisfaction problem (CSP) of a constraint language if it is complete and has the variable elimination property (VEP). However, we also show that no complete VEP constraint language can have a domain with more than 2 values. We then present a simple variant of the DPC algorithm, called DPC*, and show that the CSP of a constraint language can be decided by DPC* if it is closed under a majority operation. In fact, DPC* is sufficient for guaranteeing backtrack-free search for such constraint networks. Examples of majority-closed constraint classes include the classes of connected row-convex (CRC) constraints and tree-preserving constraints, which have found applications in various domains, such as scene labeling, temporal reasoning, geometric reasoning, and logical filtering. Our experimental evaluations show that DPC* significantly outperforms the state-of-the-art algorithms for solving majority-closed constraints.