Clustering by Mining Density Distributions and Splitting Manifold Structure

Spectral clustering requires the time-consuming decomposition of the Laplacian matrix of the similarity graph, thus limiting its applicability to large datasets. To improve the efficiency of spectral clustering, a top-down approach was recently proposed, which first divides the data into several micro-clusters (granular-balls), then splits these micro-clusters when they are not "compact'', and finally uses these micro-clusters as nodes to construct a similarity graph for more efficient spectral clustering. However, this top-down approach is challenging to adapt to unevenly distributed or structurally complex data. This is because constructing micro-clusters as a rough ball struggles to capture the shape and structure of data in a local range, and the simplistic splitting rule that solely targets ``compactness'' is susceptible to noise and variations in data density and leads to micro-clusters with varying shapes, making it challenging to accurately measure the similarity between them. To resolve these issues, this paper first proposes to start from local structures to obtain micro-clusters, such that the complex structural information inside local neighborhoods is well captured by them. Moreover, by noting that Euclidean distance is more suitable for convex sets, this paper further proposes a data splitting rule that couples local density and data manifold structures, so that the similarities of the obtained micro-clusters can be easily characterized. A novel similarity measure between micro-clusters is then proposed for the final spectral clustering. A series of experiments based on synthetic and real-world datasets demonstrate that the proposed method has better adaptability to structurally complex data than granular-ball based methods.

TANGO: Clustering with Typicality-Aware Nonlocal Mode-Seeking and Graph-Cut Optimization

Density-based clustering methods by mode-seeking usually achieve clustering by using local density estimation to mine structural information, such as local dependencies from lower density points to higher neighbors. However, they often rely too heavily on \emph{local} structures and neglect \emph{global} characteristics, which can lead to significant errors in peak selection and dependency establishment. Although introducing more hyperparameters that revise dependencies can help mitigate this issue, tuning them is challenging and even impossible on real-world datasets. In this paper, we propose a new algorithm (TANGO) to establish local dependencies by exploiting a global-view \emph{typicality} of points, which is obtained by mining further the density distributions and initial dependencies. TANGO then obtains sub-clusters with the help of the adjusted dependencies, and characterizes the similarity between sub-clusters by incorporating path-based connectivity. It achieves final clustering by employing graph-cut on sub-clusters, thus avoiding the challenging selection of cluster centers. Moreover, this paper provides theoretical analysis and an efficient method for the calculation of typicality. Experimental results on several synthetic and $16$ real-world datasets demonstrate the effectiveness and superiority of TANGO.

On Distributive Subalgebras of Qualitative Spatial and Temporal Calculi

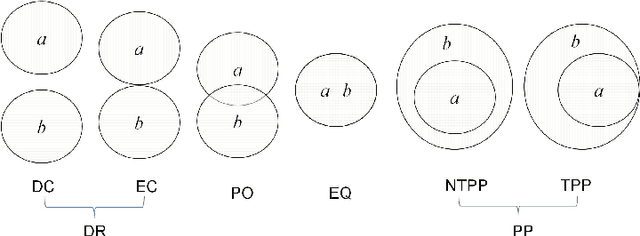
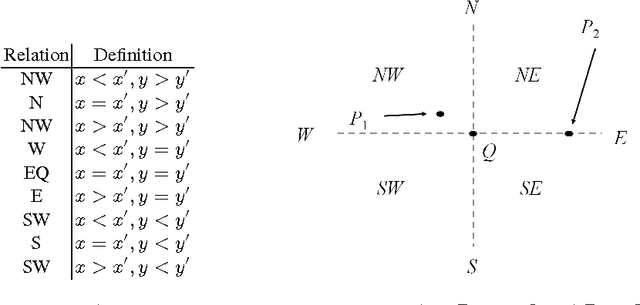
Qualitative calculi play a central role in representing and reasoning about qualitative spatial and temporal knowledge. This paper studies distributive subalgebras of qualitative calculi, which are subalgebras in which (weak) composition distributives over nonempty intersections. It has been proven for RCC5 and RCC8 that path consistent constraint network over a distributive subalgebra is always minimal and globally consistent (in the sense of strong $n$-consistency) in a qualitative sense. The well-known subclass of convex interval relations provides one such an example of distributive subalgebras. This paper first gives a characterisation of distributive subalgebras, which states that the intersection of a set of $n\geq 3$ relations in the subalgebra is nonempty if and only if the intersection of every two of these relations is nonempty. We further compute and generate all maximal distributive subalgebras for Point Algebra, Interval Algebra, RCC5 and RCC8, Cardinal Relation Algebra, and Rectangle Algebra. Lastly, we establish two nice properties which will play an important role in efficient reasoning with constraint networks involving a large number of variables.

On Redundant Topological Constraints

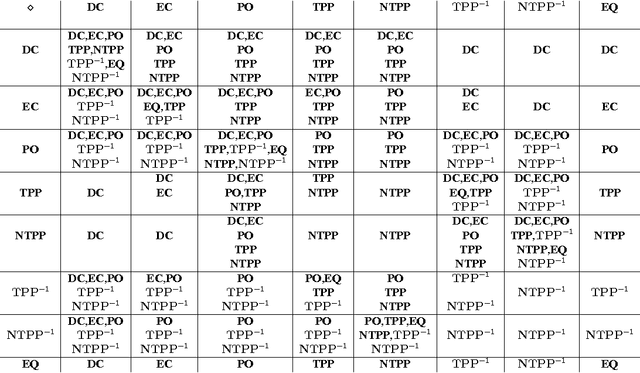
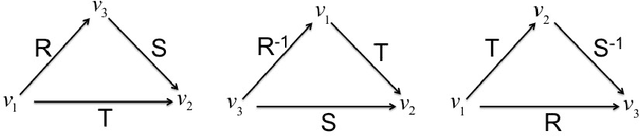
The Region Connection Calculus (RCC) is a well-known calculus for representing part-whole and topological relations. It plays an important role in qualitative spatial reasoning, geographical information science, and ontology. The computational complexity of reasoning with RCC5 and RCC8 (two fragments of RCC) as well as other qualitative spatial/temporal calculi has been investigated in depth in the literature. Most of these works focus on the consistency of qualitative constraint networks. In this paper, we consider the important problem of redundant qualitative constraints. For a set $\Gamma$ of qualitative constraints, we say a constraint $(x R y)$ in $\Gamma$ is redundant if it is entailed by the rest of $\Gamma$. A prime subnetwork of $\Gamma$ is a subset of $\Gamma$ which contains no redundant constraints and has the same solution set as $\Gamma$. It is natural to ask how to compute such a prime subnetwork, and when it is unique. In this paper, we show that this problem is in general intractable, but becomes tractable if $\Gamma$ is over a tractable subalgebra $\mathcal{S}$ of a qualitative calculus. Furthermore, if $\mathcal{S}$ is a subalgebra of RCC5 or RCC8 in which weak composition distributes over nonempty intersections, then $\Gamma$ has a unique prime subnetwork, which can be obtained in cubic time by removing all redundant constraints simultaneously from $\Gamma$. As a byproduct, we show that any path-consistent network over such a distributive subalgebra is weakly globally consistent and minimal. A thorough empirical analysis of the prime subnetwork upon real geographical data sets demonstrates the approach is able to identify significantly more redundant constraints than previously proposed algorithms, especially in constraint networks with larger proportions of partial overlap relations.