Activity-based and agent-based Transport model of Melbourne (AToM): an open multi-modal transport simulation model for Greater Melbourne

Agent-based and activity-based models for simulating transportation systems have attracted significant attention in recent years. Few studies, however, include a detailed representation of active modes of transportation - such as walking and cycling - at a city-wide level, where dominating motorised modes are often of primary concern. This paper presents an open workflow for creating a multi-modal agent-based and activity-based transport simulation model, focusing on Greater Melbourne, and including the process of mode choice calibration for the four main travel modes of driving, public transport, cycling and walking. The synthetic population generated and used as an input for the simulation model represented Melbourne's population based on Census 2016, with daily activities and trips based on the Victoria's 2016-18 travel survey data. The road network used in the simulation model includes all public roads accessible via the included travel modes. We compared the output of the simulation model with observations from the real world in terms of mode share, road volume, travel time, and travel distance. Through these comparisons, we showed that our model is suitable for studying mode choice and road usage behaviour of travellers.

An Activity-Based Model of Transport Demand for Greater Melbourne

In this paper, we present an algorithm for creating a synthetic population for the Greater Melbourne area using a combination of machine learning, probabilistic, and gravity-based approaches. We combine these techniques in a hybrid model with three primary innovations: 1. when assigning activity patterns, we generate individual activity chains for every agent, tailored to their cohort; 2. when selecting destinations, we aim to strike a balance between the distance-decay of trip lengths and the activity-based attraction of destination locations; and 3. we take into account the number of trips remaining for an agent so as to ensure they do not select a destination that would be unreasonable to return home from. Our method is completely open and replicable, requiring only publicly available data to generate a synthetic population of agents compatible with commonly used agent-based modeling software such as MATSim. The synthetic population was found to be accurate in terms of distance distribution, mode choice, and destination choice for a variety of population sizes.

On Redundant Topological Constraints

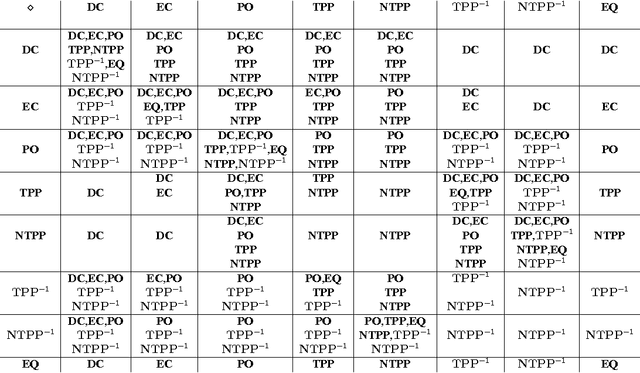
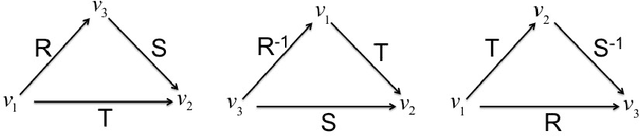
The Region Connection Calculus (RCC) is a well-known calculus for representing part-whole and topological relations. It plays an important role in qualitative spatial reasoning, geographical information science, and ontology. The computational complexity of reasoning with RCC5 and RCC8 (two fragments of RCC) as well as other qualitative spatial/temporal calculi has been investigated in depth in the literature. Most of these works focus on the consistency of qualitative constraint networks. In this paper, we consider the important problem of redundant qualitative constraints. For a set $\Gamma$ of qualitative constraints, we say a constraint $(x R y)$ in $\Gamma$ is redundant if it is entailed by the rest of $\Gamma$. A prime subnetwork of $\Gamma$ is a subset of $\Gamma$ which contains no redundant constraints and has the same solution set as $\Gamma$. It is natural to ask how to compute such a prime subnetwork, and when it is unique. In this paper, we show that this problem is in general intractable, but becomes tractable if $\Gamma$ is over a tractable subalgebra $\mathcal{S}$ of a qualitative calculus. Furthermore, if $\mathcal{S}$ is a subalgebra of RCC5 or RCC8 in which weak composition distributes over nonempty intersections, then $\Gamma$ has a unique prime subnetwork, which can be obtained in cubic time by removing all redundant constraints simultaneously from $\Gamma$. As a byproduct, we show that any path-consistent network over such a distributive subalgebra is weakly globally consistent and minimal. A thorough empirical analysis of the prime subnetwork upon real geographical data sets demonstrates the approach is able to identify significantly more redundant constraints than previously proposed algorithms, especially in constraint networks with larger proportions of partial overlap relations.