On Redundant Topological Constraints
Paper and Code
Feb 13, 2015

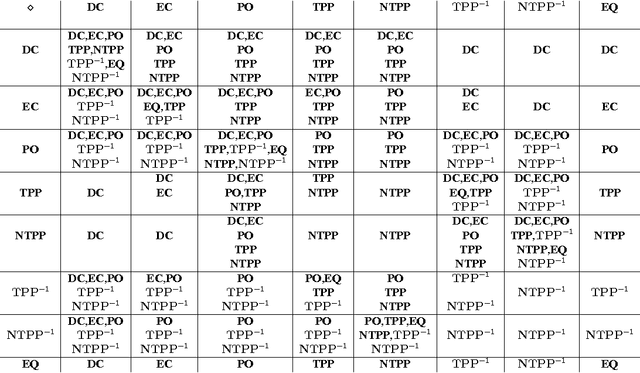
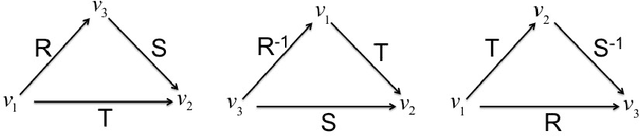
The Region Connection Calculus (RCC) is a well-known calculus for representing part-whole and topological relations. It plays an important role in qualitative spatial reasoning, geographical information science, and ontology. The computational complexity of reasoning with RCC5 and RCC8 (two fragments of RCC) as well as other qualitative spatial/temporal calculi has been investigated in depth in the literature. Most of these works focus on the consistency of qualitative constraint networks. In this paper, we consider the important problem of redundant qualitative constraints. For a set $\Gamma$ of qualitative constraints, we say a constraint $(x R y)$ in $\Gamma$ is redundant if it is entailed by the rest of $\Gamma$. A prime subnetwork of $\Gamma$ is a subset of $\Gamma$ which contains no redundant constraints and has the same solution set as $\Gamma$. It is natural to ask how to compute such a prime subnetwork, and when it is unique. In this paper, we show that this problem is in general intractable, but becomes tractable if $\Gamma$ is over a tractable subalgebra $\mathcal{S}$ of a qualitative calculus. Furthermore, if $\mathcal{S}$ is a subalgebra of RCC5 or RCC8 in which weak composition distributes over nonempty intersections, then $\Gamma$ has a unique prime subnetwork, which can be obtained in cubic time by removing all redundant constraints simultaneously from $\Gamma$. As a byproduct, we show that any path-consistent network over such a distributive subalgebra is weakly globally consistent and minimal. A thorough empirical analysis of the prime subnetwork upon real geographical data sets demonstrates the approach is able to identify significantly more redundant constraints than previously proposed algorithms, especially in constraint networks with larger proportions of partial overlap relations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge