A Fast Algorithm for Computing the Deficiency Number of a Mahjong Hand

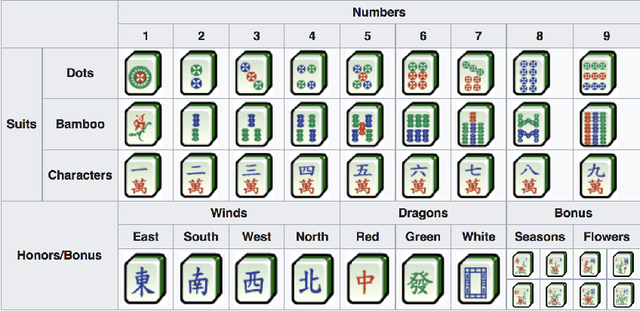
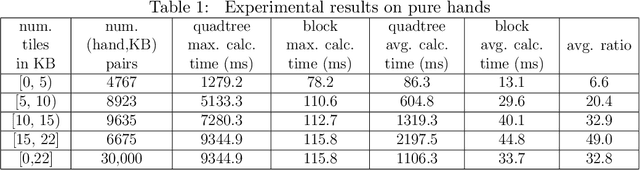
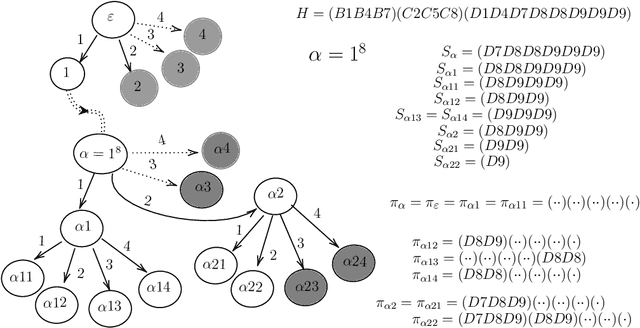
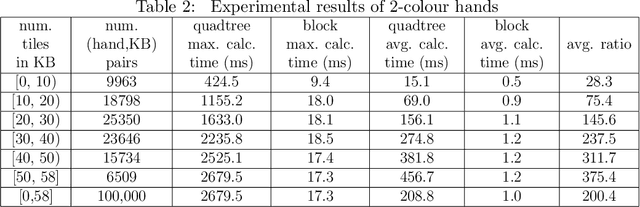
The tile-based multiplayer game Mahjong is widely played in Asia and has also become increasingly popular worldwide. Face-to-face or online, each player begins with a hand of 13 tiles and players draw and discard tiles in turn until they complete a winning hand. An important notion in Mahjong is the deficiency number (a.k.a. shanten number in Japanese Mahjong) of a hand, which estimates how many tile changes are necessary to complete the hand into a winning hand. The deficiency number plays an essential role in major decision-making tasks such as selecting a tile to discard. This paper proposes a fast algorithm for computing the deficiency number of a Mahjong hand. Compared with the baseline algorithm, the new algorithm is usually 100 times faster and, more importantly, respects the agent's knowledge about available tiles. The algorithm can be used as a basic procedure in all Mahjong variants by both rule-based and machine learning-based Mahjong AI.

Let's Play Mahjong!

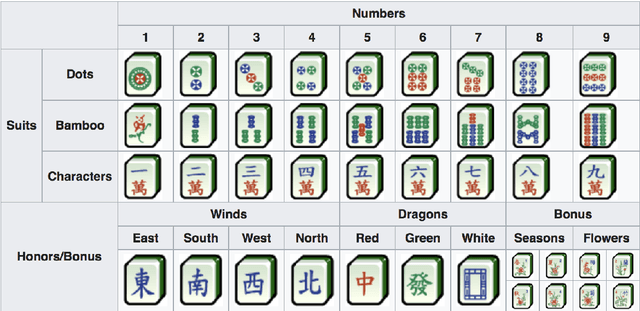
Mahjong is a very popular tile-based game commonly played by four players. Each player begins with a hand of 13 tiles and, in turn, players draw and discard (i.e., change) tiles until they complete a legal hand using a 14th tile. In this paper, we initiate a mathematical and AI study of the Mahjong game and try to answer two fundamental questions: how bad is a hand of 14 tiles? and which tile should I discard? We define and characterise the notion of deficiency and present an optimal policy to discard a tile in order to increase the chance of completing a legal hand within $k$ tile changes for each $k\geq 1$.

Multiagent Simple Temporal Problem: The Arc-Consistency Approach

The Simple Temporal Problem (STP) is a fundamental temporal reasoning problem and has recently been extended to the Multiagent Simple Temporal Problem (MaSTP). In this paper we present a novel approach that is based on enforcing arc-consistency (AC) on the input (multiagent) simple temporal network. We show that the AC-based approach is sufficient for solving both the STP and MaSTP and provide efficient algorithms for them. As our AC-based approach does not impose new constraints between agents, it does not violate the privacy of the agents and is superior to the state-of-the-art approach to MaSTP. Empirical evaluations on diverse benchmark datasets also show that our AC-based algorithms for STP and MaSTP are significantly more efficient than existing approaches.

Exploring Directional Path-Consistency for Solving Constraint Networks

Among the local consistency techniques used for solving constraint networks, path-consistency (PC) has received a great deal of attention. However, enforcing PC is computationally expensive and sometimes even unnecessary. Directional path-consistency (DPC) is a weaker notion of PC that considers a given variable ordering and can thus be enforced more efficiently than PC. This paper shows that DPC (the DPC enforcing algorithm of Dechter and Pearl) decides the constraint satisfaction problem (CSP) of a constraint language if it is complete and has the variable elimination property (VEP). However, we also show that no complete VEP constraint language can have a domain with more than 2 values. We then present a simple variant of the DPC algorithm, called DPC*, and show that the CSP of a constraint language can be decided by DPC* if it is closed under a majority operation. In fact, DPC* is sufficient for guaranteeing backtrack-free search for such constraint networks. Examples of majority-closed constraint classes include the classes of connected row-convex (CRC) constraints and tree-preserving constraints, which have found applications in various domains, such as scene labeling, temporal reasoning, geometric reasoning, and logical filtering. Our experimental evaluations show that DPC* significantly outperforms the state-of-the-art algorithms for solving majority-closed constraints.

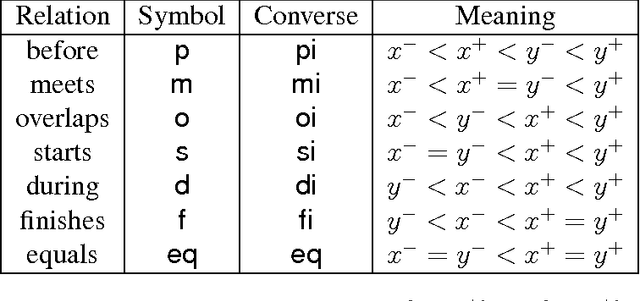
On Distributive Subalgebras of Qualitative Spatial and Temporal Calculi

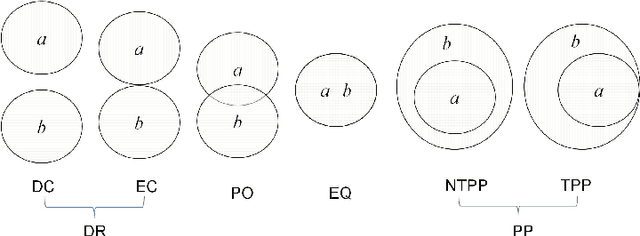
Qualitative calculi play a central role in representing and reasoning about qualitative spatial and temporal knowledge. This paper studies distributive subalgebras of qualitative calculi, which are subalgebras in which (weak) composition distributives over nonempty intersections. It has been proven for RCC5 and RCC8 that path consistent constraint network over a distributive subalgebra is always minimal and globally consistent (in the sense of strong $n$-consistency) in a qualitative sense. The well-known subclass of convex interval relations provides one such an example of distributive subalgebras. This paper first gives a characterisation of distributive subalgebras, which states that the intersection of a set of $n\geq 3$ relations in the subalgebra is nonempty if and only if the intersection of every two of these relations is nonempty. We further compute and generate all maximal distributive subalgebras for Point Algebra, Interval Algebra, RCC5 and RCC8, Cardinal Relation Algebra, and Rectangle Algebra. Lastly, we establish two nice properties which will play an important role in efficient reasoning with constraint networks involving a large number of variables.

On Redundant Topological Constraints

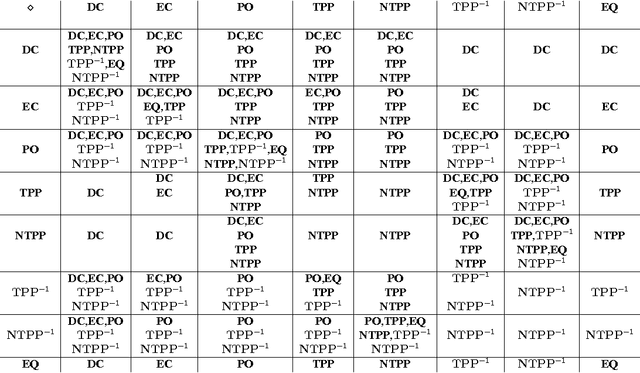
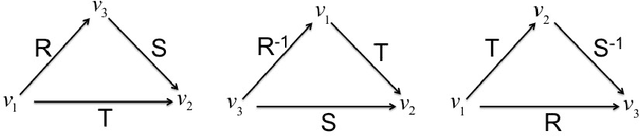
The Region Connection Calculus (RCC) is a well-known calculus for representing part-whole and topological relations. It plays an important role in qualitative spatial reasoning, geographical information science, and ontology. The computational complexity of reasoning with RCC5 and RCC8 (two fragments of RCC) as well as other qualitative spatial/temporal calculi has been investigated in depth in the literature. Most of these works focus on the consistency of qualitative constraint networks. In this paper, we consider the important problem of redundant qualitative constraints. For a set $\Gamma$ of qualitative constraints, we say a constraint $(x R y)$ in $\Gamma$ is redundant if it is entailed by the rest of $\Gamma$. A prime subnetwork of $\Gamma$ is a subset of $\Gamma$ which contains no redundant constraints and has the same solution set as $\Gamma$. It is natural to ask how to compute such a prime subnetwork, and when it is unique. In this paper, we show that this problem is in general intractable, but becomes tractable if $\Gamma$ is over a tractable subalgebra $\mathcal{S}$ of a qualitative calculus. Furthermore, if $\mathcal{S}$ is a subalgebra of RCC5 or RCC8 in which weak composition distributes over nonempty intersections, then $\Gamma$ has a unique prime subnetwork, which can be obtained in cubic time by removing all redundant constraints simultaneously from $\Gamma$. As a byproduct, we show that any path-consistent network over such a distributive subalgebra is weakly globally consistent and minimal. A thorough empirical analysis of the prime subnetwork upon real geographical data sets demonstrates the approach is able to identify significantly more redundant constraints than previously proposed algorithms, especially in constraint networks with larger proportions of partial overlap relations.

Realizing RCC8 networks using convex regions

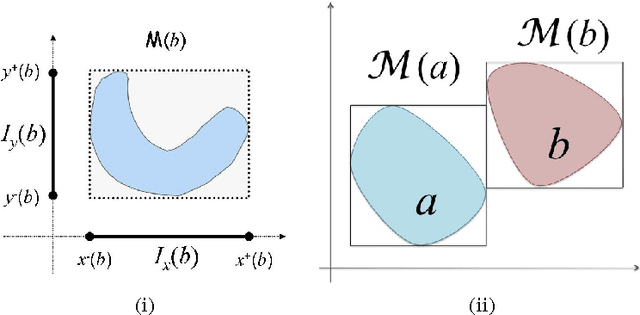
RCC8 is a popular fragment of the region connection calculus, in which qualitative spatial relations between regions, such as adjacency, overlap and parthood, can be expressed. While RCC8 is essentially dimensionless, most current applications are confined to reasoning about two-dimensional or three-dimensional physical space. In this paper, however, we are mainly interested in conceptual spaces, which typically are high-dimensional Euclidean spaces in which the meaning of natural language concepts can be represented using convex regions. The aim of this paper is to analyze how the restriction to convex regions constrains the realizability of networks of RCC8 relations. First, we identify all ways in which the set of RCC8 base relations can be restricted to guarantee that consistent networks can be convexly realized in respectively 1D, 2D, 3D, and 4D. Most surprisingly, we find that if the relation 'partially overlaps' is disallowed, all consistent atomic RCC8 networks can be convexly realized in 4D. If instead refinements of the relation 'part of' are disallowed, all consistent atomic RCC8 relations can be convexly realized in 3D. We furthermore show, among others, that any consistent RCC8 network with 2n+1 variables can be realized using convex regions in the n-dimensional Euclidean space.

On the Internal Topological Structure of Plane Regions

The study of topological information of spatial objects has for a long time been a focus of research in disciplines like computational geometry, spatial reasoning, cognitive science, and robotics. While the majority of these researches emphasised the topological relations between spatial objects, this work studies the internal topological structure of bounded plane regions, which could consist of multiple pieces and/or have holes and islands to any finite level. The insufficiency of simple regions (regions homeomorphic to closed disks) to cope with the variety and complexity of spatial entities and phenomena has been widely acknowledged. Another significant drawback of simple regions is that they are not closed under set operations union, intersection, and difference. This paper considers bounded semi-algebraic regions, which are closed under set operations and can closely approximate most plane regions arising in practice.

On A Semi-Automatic Method for Generating Composition Tables

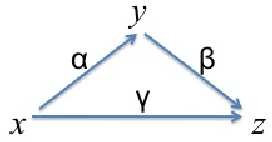
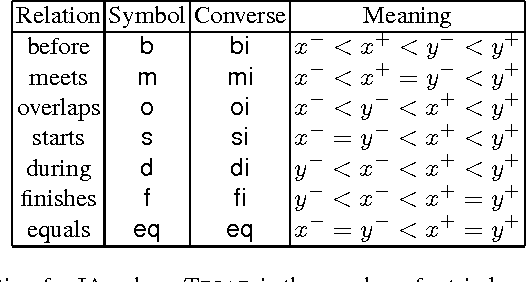
Originating from Allen's Interval Algebra, composition-based reasoning has been widely acknowledged as the most popular reasoning technique in qualitative spatial and temporal reasoning. Given a qualitative calculus (i.e. a relation model), the first thing we should do is to establish its composition table (CT). In the past three decades, such work is usually done manually. This is undesirable and error-prone, given that the calculus may contain tens or hundreds of basic relations. Computing the correct CT has been identified by Tony Cohn as a challenge for computer scientists in 1995. This paper addresses this problem and introduces a semi-automatic method to compute the CT by randomly generating triples of elements. For several important qualitative calculi, our method can establish the correct CT in a reasonable short time. This is illustrated by applications to the Interval Algebra, the Region Connection Calculus RCC-8, the INDU calculus, and the Oriented Point Relation Algebras. Our method can also be used to generate CTs for customised qualitative calculi defined on restricted domains.

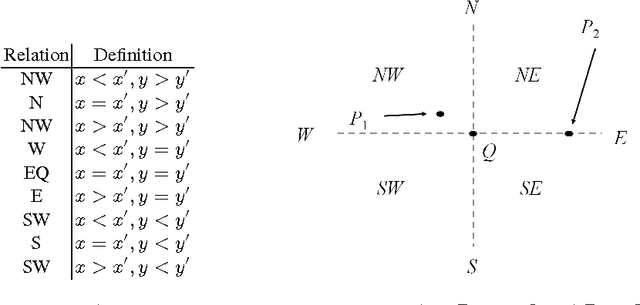
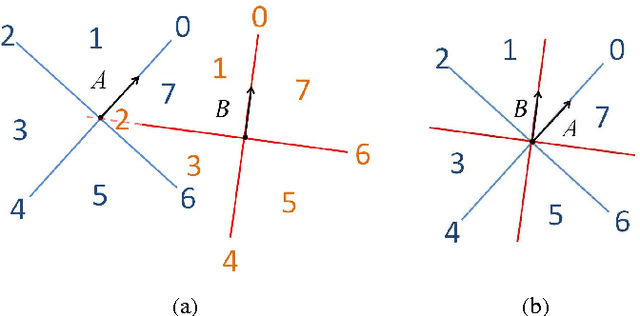
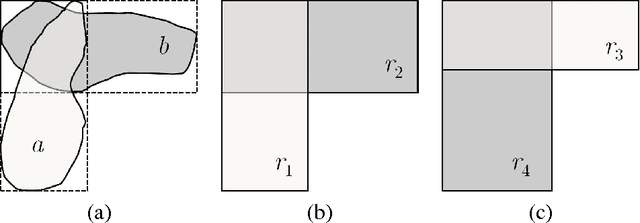
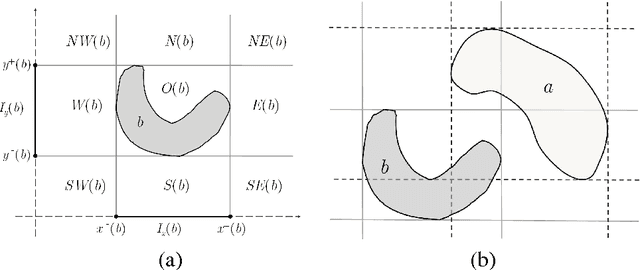
Reasoning about Cardinal Directions between Extended Objects: The Hardness Result

The cardinal direction calculus (CDC) proposed by Goyal and Egenhofer is a very expressive qualitative calculus for directional information of extended objects. Early work has shown that consistency checking of complete networks of basic CDC constraints is tractable while reasoning with the CDC in general is NP-hard. This paper shows, however, if allowing some constraints unspecified, then consistency checking of possibly incomplete networks of basic CDC constraints is already intractable. This draws a sharp boundary between the tractable and intractable subclasses of the CDC. The result is achieved by a reduction from the well-known 3-SAT problem.