On A Semi-Automatic Method for Generating Composition Tables
Paper and Code
May 21, 2011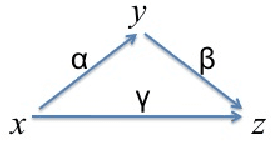
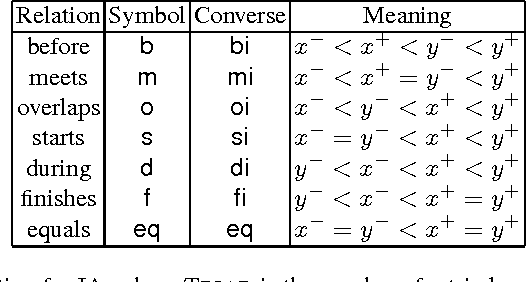
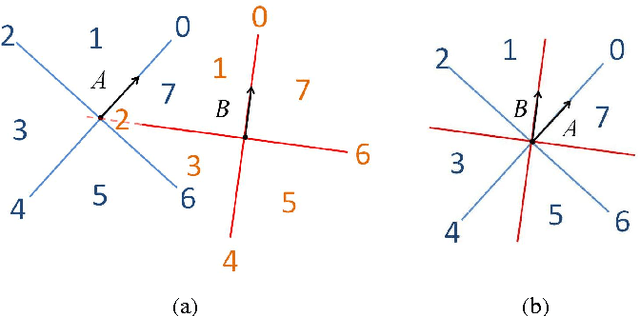

Originating from Allen's Interval Algebra, composition-based reasoning has been widely acknowledged as the most popular reasoning technique in qualitative spatial and temporal reasoning. Given a qualitative calculus (i.e. a relation model), the first thing we should do is to establish its composition table (CT). In the past three decades, such work is usually done manually. This is undesirable and error-prone, given that the calculus may contain tens or hundreds of basic relations. Computing the correct CT has been identified by Tony Cohn as a challenge for computer scientists in 1995. This paper addresses this problem and introduces a semi-automatic method to compute the CT by randomly generating triples of elements. For several important qualitative calculi, our method can establish the correct CT in a reasonable short time. This is illustrated by applications to the Interval Algebra, the Region Connection Calculus RCC-8, the INDU calculus, and the Oriented Point Relation Algebras. Our method can also be used to generate CTs for customised qualitative calculi defined on restricted domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge