A Fast Algorithm for Computing the Deficiency Number of a Mahjong Hand

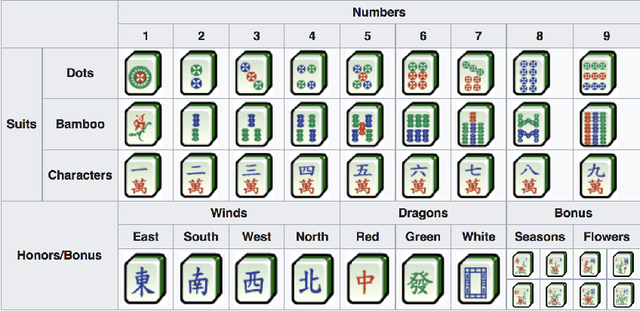
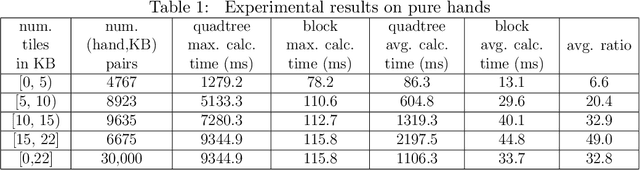
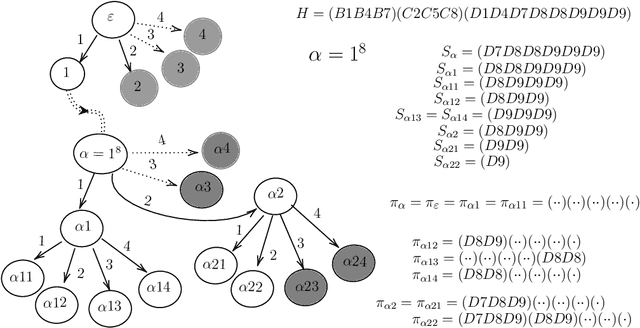
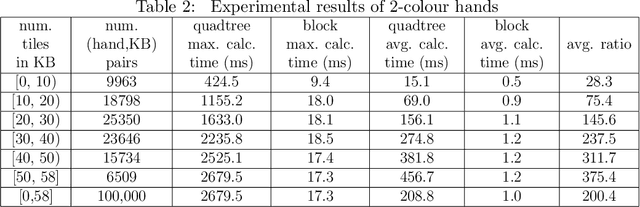
The tile-based multiplayer game Mahjong is widely played in Asia and has also become increasingly popular worldwide. Face-to-face or online, each player begins with a hand of 13 tiles and players draw and discard tiles in turn until they complete a winning hand. An important notion in Mahjong is the deficiency number (a.k.a. shanten number in Japanese Mahjong) of a hand, which estimates how many tile changes are necessary to complete the hand into a winning hand. The deficiency number plays an essential role in major decision-making tasks such as selecting a tile to discard. This paper proposes a fast algorithm for computing the deficiency number of a Mahjong hand. Compared with the baseline algorithm, the new algorithm is usually 100 times faster and, more importantly, respects the agent's knowledge about available tiles. The algorithm can be used as a basic procedure in all Mahjong variants by both rule-based and machine learning-based Mahjong AI.

Let's Play Mahjong!

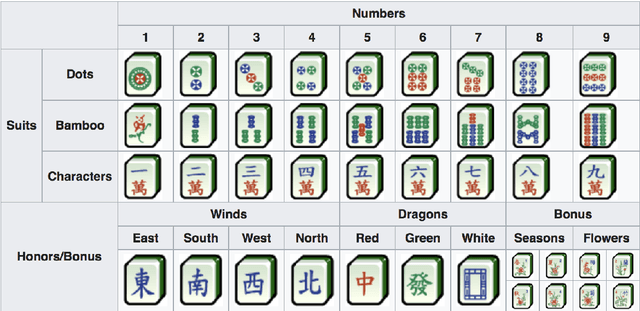
Mahjong is a very popular tile-based game commonly played by four players. Each player begins with a hand of 13 tiles and, in turn, players draw and discard (i.e., change) tiles until they complete a legal hand using a 14th tile. In this paper, we initiate a mathematical and AI study of the Mahjong game and try to answer two fundamental questions: how bad is a hand of 14 tiles? and which tile should I discard? We define and characterise the notion of deficiency and present an optimal policy to discard a tile in order to increase the chance of completing a legal hand within $k$ tile changes for each $k\geq 1$.