Reasoning about Cardinal Directions between Extended Objects: The Hardness Result
Paper and Code
Nov 04, 2010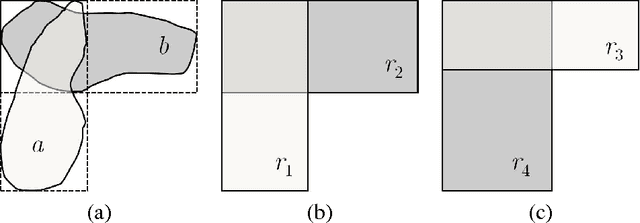

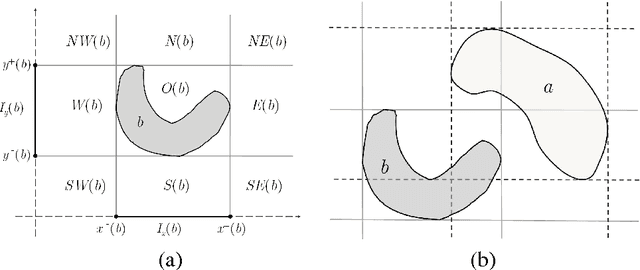
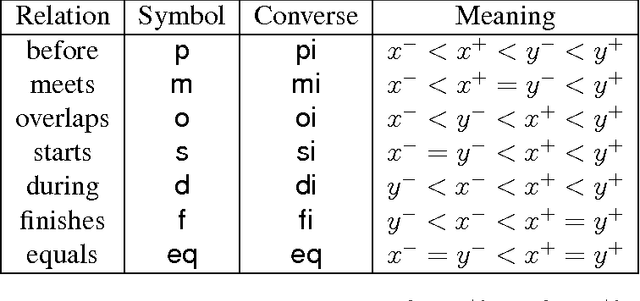
The cardinal direction calculus (CDC) proposed by Goyal and Egenhofer is a very expressive qualitative calculus for directional information of extended objects. Early work has shown that consistency checking of complete networks of basic CDC constraints is tractable while reasoning with the CDC in general is NP-hard. This paper shows, however, if allowing some constraints unspecified, then consistency checking of possibly incomplete networks of basic CDC constraints is already intractable. This draws a sharp boundary between the tractable and intractable subclasses of the CDC. The result is achieved by a reduction from the well-known 3-SAT problem.
* 24 pages, 24 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge