Compiling Metric Temporal Answer Set Programming

We develop a computational approach to Metric Answer Set Programming (ASP) to allow for expressing quantitative temporal constrains, like durations and deadlines. A central challenge is to maintain scalability when dealing with fine-grained timing constraints, which can significantly exacerbate ASP's grounding bottleneck. To address this issue, we leverage extensions of ASP with difference constraints, a simplified form of linear constraints, to handle time-related aspects externally. Our approach effectively decouples metric ASP from the granularity of time, resulting in a solution that is unaffected by time precision.

Computational methods for Dynamic Answer Set Programming

In our daily lives and industrial settings, we often encounter dynamic problems that require reasoning over time and metric constraints. These include tasks such as scheduling, routing, and production sequencing. Dynamic logics have traditionally addressed these needs but often lack the flexibility and integration required for comprehensive problem modeling. This research aims to extend Answer Set Programming (ASP), a powerful declarative problem-solving approach, to handle dynamic domains effectively. By integrating concepts from dynamic, temporal, and metric logics into ASP, we seek to develop robust systems capable of modeling complex dynamic problems and performing efficient reasoning tasks, thereby enhancing ASPs applicability in industrial contexts.

ASP-driven User-interaction with Clinguin

We present clinguin, a system for ASP-driven user interface design. Clinguin streamlines the development of user interfaces for ASP developers by letting them build interactive prototypes directly in ASP, eliminating the need for separate frontend languages. To this end, clinguin uses a few dedicated predicates to define user interfaces and the treatment of user-triggered events. This simple design greatly facilitates the specification of user interactions with an ASP system, in our case clingo.

Reasoning about Study Regulations in Answer Set Programming

We are interested in automating reasoning with and about study regulations, catering to various stakeholders, ranging from administrators, over faculty, to students at different stages. Our work builds on an extensive analysis of various study programs at the University of Potsdam. The conceptualization of the underlying principles provides us with a formal account of study regulations. In particular, the formalization reveals the properties of admissible study plans. With these at end, we propose an encoding of study regulations in Answer Set Programming that produces corresponding study plans. Finally, we show how this approach can be extended to a generic user interface for exploring study plans.

$\textit{Clingraph}$: A System for ASP-based Visualization

We present the ASP-based visualization tool $\textit{clingraph}$ which aims at visualizing various concepts of ASP by means of ASP itself. This idea traces back to the $\textit{aspviz}$ tool and $\textit{clingraph}$ redevelops and extends it in the context of modern ASP systems. More precisely, $\textit{clingraph}$ takes graph specifications in terms of ASP facts and hands them over to the graph visualization system $\textit{graphviz}$. The use of ASP provides a great interface between logic programs and/or answer sets and their visualization. Also, $\textit{clingraph}$ offers a $\textit{python}$ API that extends this ease of interfacing to $\textit{clingo}$'s API, and in turn to connect and monitor various aspects of the solving process.

plingo: A system for probabilistic reasoning in clingo based on lpmln

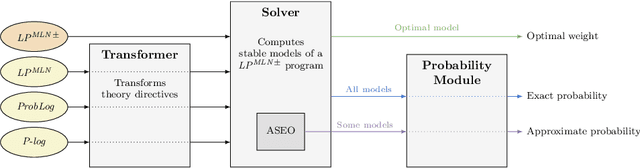
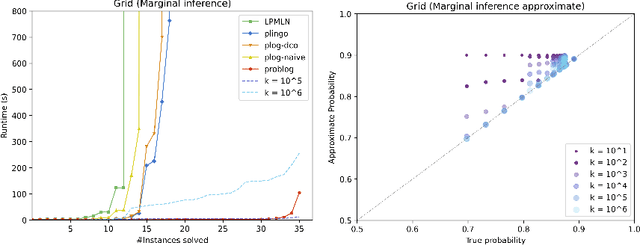
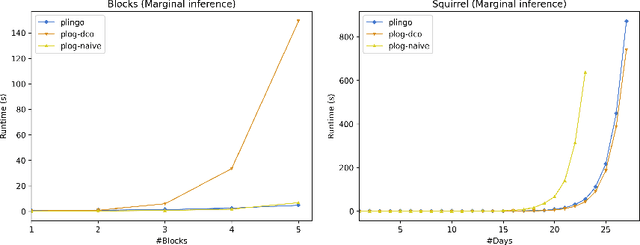
We present plingo, an extension of the ASP system clingo with various probabilistic reasoning modes. Plingo is centered upon LP^MLN, a probabilistic extension of ASP based on a weight scheme from Markov Logic. This choice is motivated by the fact that the core probabilistic reasoning modes can be mapped onto optimization problems and that LP^MLN may serve as a middle-ground formalism connecting to other probabilistic approaches. As a result, plingo offers three alternative frontends, for LP^MLN, P-log, and ProbLog. The corresponding input languages and reasoning modes are implemented by means of clingo's multi-shot and theory solving capabilities. The core of plingo amounts to a re-implementation of LP^MLN in terms of modern ASP technology, extended by an approximation technique based on a new method for answer set enumeration in the order of optimality. We evaluate plingo's performance empirically by comparing it to other probabilistic systems.

Automata Techniques for Temporal Answer Set Programming

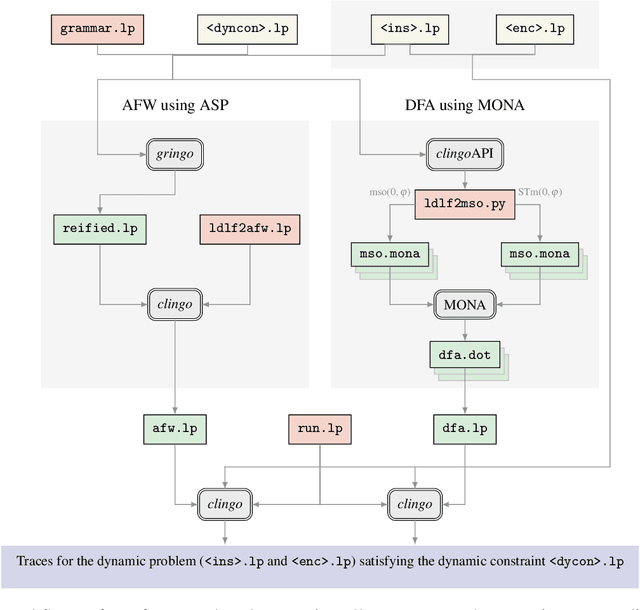
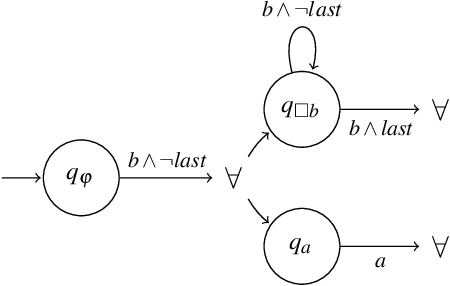
Temporal and dynamic extensions of Answer Set Programming (ASP) have played an important role in addressing dynamic problems, as they allow the use of temporal operators to reason with dynamic scenarios in a very effective way. In my Ph.D. research, I intend to exploit the relationship between automata theory and dynamic logic to add automata-based techniques to the ASP solver CLINGO helping us to deal with theses type of problems.

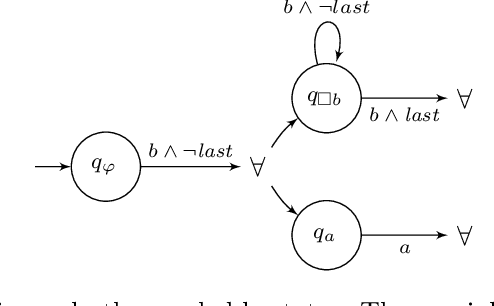
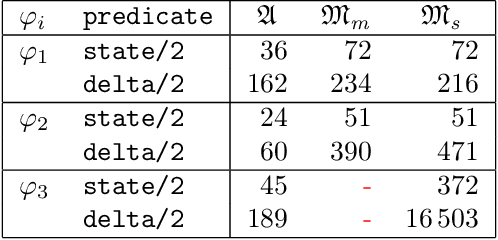
Automata for dynamic answer set solving: Preliminary report

We explore different ways of implementing temporal constraints expressed in an extension of Answer Set Programming (ASP) with language constructs from dynamic logic. Foremost, we investigate how automata can be used for enforcing such constraints. The idea is to transform a dynamic constraint into an automaton expressed in terms of a logic program that enforces the satisfaction of the original constraint. What makes this approach attractive is its independence of time stamps and the potential to detect unsatisfiability. On the one hand, we elaborate upon a transformation of dynamic formulas into alternating automata that relies on meta-programming in ASP. This is the first application of reification applied to theory expressions in gringo. On the other hand, we propose two transformations of dynamic formulas into monadic second-order formulas. These can then be used by off-the-shelf tools to construct the corresponding automata. We contrast both approaches empirically with the one of the temporal ASP solver telingo that directly maps dynamic constraints to logic programs. Since this preliminary study is restricted to dynamic formulas in integrity constraints, its implementations and (empirical) results readily apply to conventional linear dynamic logic, too.