Automata for dynamic answer set solving: Preliminary report
Paper and Code
Sep 04, 2021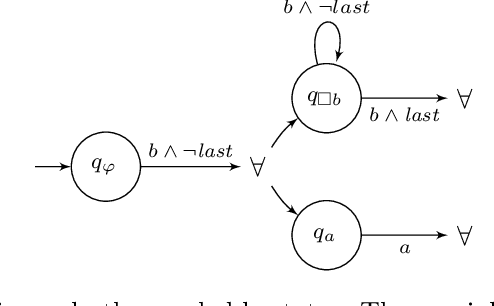


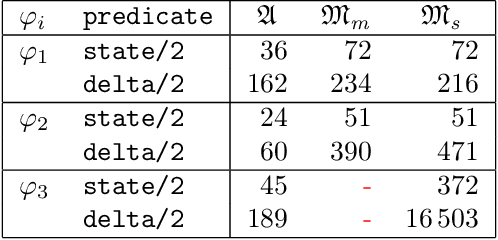
We explore different ways of implementing temporal constraints expressed in an extension of Answer Set Programming (ASP) with language constructs from dynamic logic. Foremost, we investigate how automata can be used for enforcing such constraints. The idea is to transform a dynamic constraint into an automaton expressed in terms of a logic program that enforces the satisfaction of the original constraint. What makes this approach attractive is its independence of time stamps and the potential to detect unsatisfiability. On the one hand, we elaborate upon a transformation of dynamic formulas into alternating automata that relies on meta-programming in ASP. This is the first application of reification applied to theory expressions in gringo. On the other hand, we propose two transformations of dynamic formulas into monadic second-order formulas. These can then be used by off-the-shelf tools to construct the corresponding automata. We contrast both approaches empirically with the one of the temporal ASP solver telingo that directly maps dynamic constraints to logic programs. Since this preliminary study is restricted to dynamic formulas in integrity constraints, its implementations and (empirical) results readily apply to conventional linear dynamic logic, too.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge