Metric Dynamic Equilibrium Logic

In temporal extensions of Answer Set Programming (ASP) based on linear-time, the behavior of dynamic systems is captured by sequences of states. While this representation reflects their relative order, it abstracts away the specific times associated with each state. In many applications, however, timing constraints are important like, for instance, when planning and scheduling go hand in hand. We address this by developing a metric extension of linear-time Dynamic Equilibrium Logic, in which dynamic operators are constrained by intervals over integers. The resulting Metric Dynamic Equilibrium Logic provides the foundation of an ASP-based approach for specifying qualitative and quantitative dynamic constraints. As such, it constitutes the most general among a whole spectrum of temporal extensions of Equilibrium Logic. In detail, we show that it encompasses Temporal, Dynamic, Metric, and regular Equilibrium Logic, as well as its classic counterparts once the law of the excluded middle is added.

Past-present temporal programs over finite traces

Extensions of Answer Set Programming with language constructs from temporal logics, such as temporal equilibrium logic over finite traces (TELf), provide an expressive computational framework for modeling dynamic applications. In this paper, we study the so-called past-present syntactic subclass, which consists of a set of logic programming rules whose body references to the past and head to the present. Such restriction ensures that the past remains independent of the future, which is the case in most dynamic domains. We extend the definitions of completion and loop formulas to the case of past-present formulas, which allows capturing the temporal stable models of a set of past-present temporal programs by means of an LTLf expression.

Gödel-Dummett linear temporal logic

We investigate a version of linear temporal logic whose propositional fragment is G\"odel-Dummett logic (which is well known both as a superintuitionistic logic and a t-norm fuzzy logic). We define the logic using two natural semantics: first a real-valued semantics, where statements have a degree of truth in the real unit interval and second a `bi-relational' semantics. We then show that these two semantics indeed define one and the same logic: the statements that are valid for the real-valued semantics are the same as those that are valid for the bi-relational semantics. This G\"odel temporal logic does not have any form of the finite model property for these two semantics: there are non-valid statements that can only be falsified on an infinite model. However, by using the technical notion of a quasimodel, we show that every falsifiable statement is falsifiable on a finite quasimodel, yielding an algorithm for deciding if a statement is valid or not. Later, we strengthen this decidability result by giving an algorithm that uses only a polynomial amount of memory, proving that G\"odel temporal logic is PSPACE-complete. We also provide a deductive calculus for G\"odel temporal logic, and show this calculus to be sound and complete for the above-mentioned semantics, so that all (and only) the valid statements can be proved with this calculus.

Metric Temporal Equilibrium Logic over Timed Traces

In temporal extensions of Answer Set Programming (ASP) based on linear-time, the behavior of dynamic systems is captured by sequences of states. While this representation reflects their relative order, it abstracts away the specific times associated with each state. However, timing constraints are important in many applications like, for instance, when planning and scheduling go hand in hand. We address this by developing a metric extension of linear-time temporal equilibrium logic, in which temporal operators are constrained by intervals over natural numbers. The resulting Metric Equilibrium Logic provides the foundation of an ASP-based approach for specifying qualitative and quantitative dynamic constraints. To this end, we define a translation of metric formulas into monadic first-order formulas and give a correspondence between their models in Metric Equilibrium Logic and Monadic Quantified Equilibrium Logic, respectively. Interestingly, our translation provides a blue print for implementation in terms of ASP modulo difference constraints.

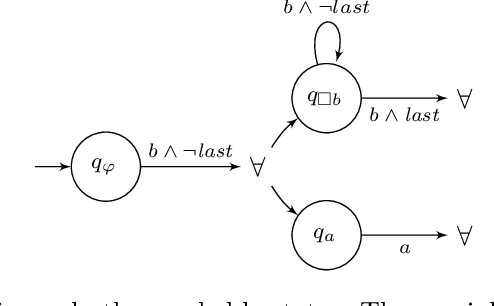
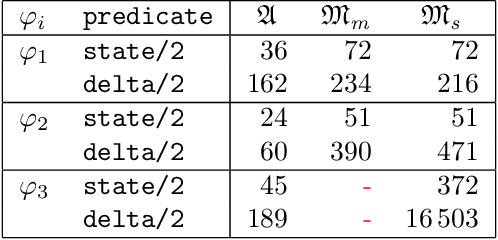
Automata for dynamic answer set solving: Preliminary report

We explore different ways of implementing temporal constraints expressed in an extension of Answer Set Programming (ASP) with language constructs from dynamic logic. Foremost, we investigate how automata can be used for enforcing such constraints. The idea is to transform a dynamic constraint into an automaton expressed in terms of a logic program that enforces the satisfaction of the original constraint. What makes this approach attractive is its independence of time stamps and the potential to detect unsatisfiability. On the one hand, we elaborate upon a transformation of dynamic formulas into alternating automata that relies on meta-programming in ASP. This is the first application of reification applied to theory expressions in gringo. On the other hand, we propose two transformations of dynamic formulas into monadic second-order formulas. These can then be used by off-the-shelf tools to construct the corresponding automata. We contrast both approaches empirically with the one of the temporal ASP solver telingo that directly maps dynamic constraints to logic programs. Since this preliminary study is restricted to dynamic formulas in integrity constraints, its implementations and (empirical) results readily apply to conventional linear dynamic logic, too.

Implementing Dynamic Answer Set Programming

We introduce an implementation of an extension of Answer Set Programming (ASP) with language constructs from dynamic (and temporal) logic that provides an expressive computational framework for modeling dynamic applications. Starting from logical foundations, provided by dynamic and temporal equilibrium logics over finite linear traces, we develop a translation of dynamic formulas into temporal logic programs. This provides us with a normal form result establishing the strong equivalence of formulas in different logics. Our translation relies on the introduction of auxiliary atoms to guarantee polynomial space complexity and to provide an embedding that is doomed to be impossible over the same language. Finally, the reduction of dynamic formulas to temporal logic programs allows us to extend ASP with both approaches in a uniform way and to implement both extensions via temporal ASP solvers such as telingo

Intuitionistic Linear Temporal Logics

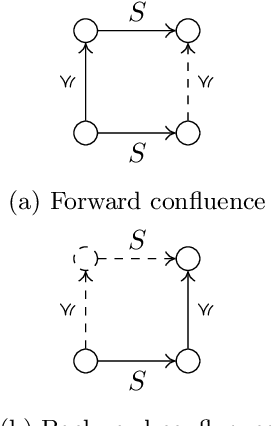
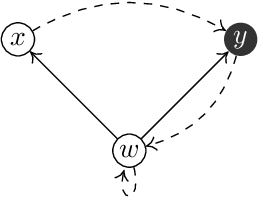
We consider intuitionistic variants of linear temporal logic with `next', `until' and `release' based on expanding posets: partial orders equipped with an order-preserving transition function. This class of structures gives rise to a logic which we denote $\iltl$, and by imposing additional constraints we obtain the logics $\itlb$ of persistent posets and $\itlht$ of here-and-there temporal logic, both of which have been considered in the literature. We prove that $\iltl$ has the effective finite model property and hence is decidable, while $\itlb$ does not have the finite model property. We also introduce notions of bounded bisimulations for these logics and use them to show that the `until' and `release' operators are not definable in terms of each other, even over the class of persistent posets.

Temporal Logic Programs with Variables

In this note we consider the problem of introducing variables in temporal logic programs under the formalism of "Temporal Equilibrium Logic" (TEL), an extension of Answer Set Programming (ASP) for dealing with linear-time modal operators. To this aim, we provide a definition of a first-order version of TEL that shares the syntax of first-order Linear-time Temporal Logic (LTL) but has a different semantics, selecting some LTL models we call "temporal stable models". Then, we consider a subclass of theories (called "splittable temporal logic programs") that are close to usual logic programs but allowing a restricted use of temporal operators. In this setting, we provide a syntactic definition of "safe variables" that suffices to show the property of "domain independence" -- that is, addition of arbitrary elements in the universe does not vary the set of temporal stable models. Finally, we present a method for computing the derivable facts by constructing a non-temporal logic program with variables that is fed to a standard ASP grounder. The information provided by the grounder is then used to generate a subset of ground temporal rules which is equivalent to (and generally smaller than) the full program instantiation.