Intuitionistic Linear Temporal Logics
Paper and Code
Dec 30, 2019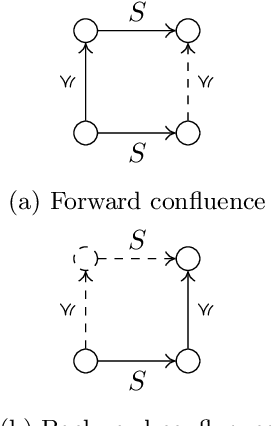
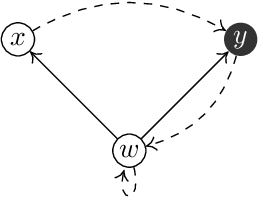


We consider intuitionistic variants of linear temporal logic with `next', `until' and `release' based on expanding posets: partial orders equipped with an order-preserving transition function. This class of structures gives rise to a logic which we denote $\iltl$, and by imposing additional constraints we obtain the logics $\itlb$ of persistent posets and $\itlht$ of here-and-there temporal logic, both of which have been considered in the literature. We prove that $\iltl$ has the effective finite model property and hence is decidable, while $\itlb$ does not have the finite model property. We also introduce notions of bounded bisimulations for these logics and use them to show that the `until' and `release' operators are not definable in terms of each other, even over the class of persistent posets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge