Learning Tree Pattern Transformations

Explaining why and how a tree $t$ structurally differs from another tree $t^*$ is a question that is encountered throughout computer science, including in understanding tree-structured data such as XML or JSON data. In this article, we explore how to learn explanations for structural differences between pairs of trees from sample data: suppose we are given a set $\{(t_1, t_1^*),\dots, (t_n, t_n^*)\}$ of pairs of labelled, ordered trees; is there a small set of rules that explains the structural differences between all pairs $(t_i, t_i^*)$? This raises two research questions: (i) what is a good notion of "rule" in this context?; and (ii) how can sets of rules explaining a data set be learnt algorithmically? We explore these questions from the perspective of database theory by (1) introducing a pattern-based specification language for tree transformations; (2) exploring the computational complexity of variants of the above algorithmic problem, e.g. showing NP-hardness for very restricted variants; and (3) discussing how to solve the problem for data from CS education research using SAT solvers.

Ontology-Mediated Querying on Databases of Bounded Cliquewidth

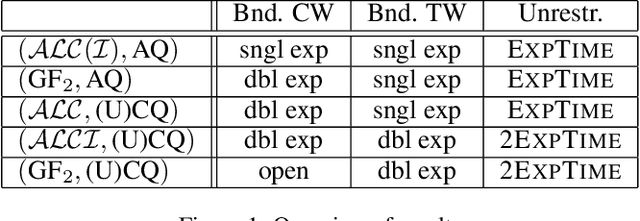
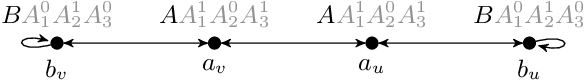
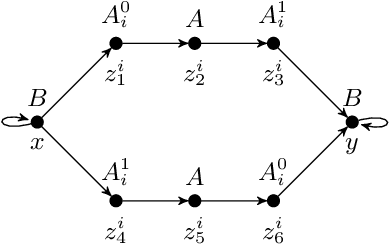
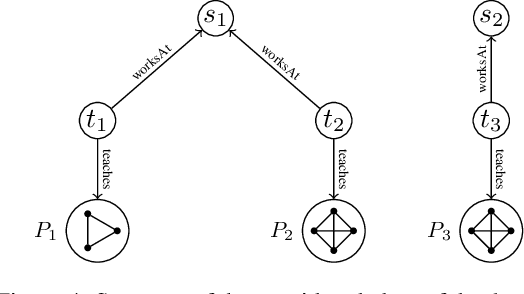
We study the evaluation of ontology-mediated queries (OMQs) on databases of bounded cliquewidth from the viewpoint of parameterized complexity theory. As the ontology language, we consider the description logics $\mathcal{ALC}$ and $\mathcal{ALCI}$ as well as the guarded two-variable fragment GF$_2$ of first-order logic. Queries are atomic queries (AQs), conjunctive queries (CQs), and unions of CQs. All studied OMQ problems are fixed-parameter linear (FPL) when the parameter is the size of the OMQ plus the cliquewidth. Our main contribution is a detailed analysis of the dependence of the running time on the parameter, exhibiting several interesting effects.

How to Approximate Ontology-Mediated Queries

We introduce and study several notions of approximation for ontology-mediated queries based on the description logics ALC and ALCI. Our approximations are of two kinds: we may (1) replace the ontology with one formulated in a tractable ontology language such as ELI or certain TGDs and (2) replace the database with one from a tractable class such as the class of databases whose treewidth is bounded by a constant. We determine the computational complexity and the relative completeness of the resulting approximations. (Almost) all of them reduce the data complexity from coNP-complete to PTime, in some cases even to fixed-parameter tractable and to linear time. While approximations of kind (1) also reduce the combined complexity, this tends to not be the case for approximations of kind (2). In some cases, the combined complexity even increases.

Query Expressibility and Verification in Ontology-Based Data Access

In ontology-based data access, multiple data sources are integrated using an ontology and mappings. In practice, this is often achieved by a bootstrapping process, that is, the ontology and mappings are first designed to support only the most important queries over the sources and then gradually extended to enable additional queries. In this paper, we study two reasoning problems that support such an approach. The expressibility problem asks whether a given source query $q_s$ is expressible as a target query (that is, over the ontology's vocabulary) and the verification problem asks, additionally given a candidate target query $q_t$, whether $q_t$ expresses $q_s$. We consider (U)CQs as source and target queries and GAV mappings, showing that both problems are $\Pi^p_2$-complete in DL-Lite, coNExpTime-complete between EL and ELHI when source queries are rooted, and 2ExpTime-complete for unrestricted source queries.

A Complete Classification of the Complexity and Rewritability of Ontology-Mediated Queries based on the Description Logic EL

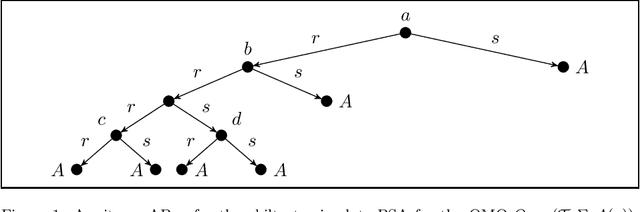
We provide an ultimately fine-grained analysis of the data complexity and rewritability of ontology-mediated queries (OMQs) based on an EL ontology and a conjunctive query (CQ). Our main results are that every such OMQ is in AC0, NL-complete, or PTime-complete and that containment in NL coincides with rewritability into linear Datalog (whereas containment in AC0 coincides with rewritability into first-order logic). We establish natural characterizations of the three cases in terms of bounded depth and (un)bounded pathwidth, and show that every of the associated meta problems such as deciding wether a given OMQ is rewritable into linear Datalog is ExpTime-complete. We also give a way to construct linear Datalog rewritings when they exist and prove that there is no constant Datalog rewritings.