How to Approximate Ontology-Mediated Queries

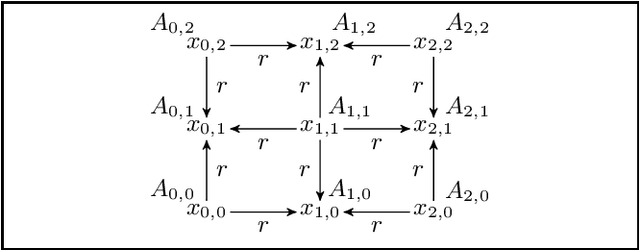
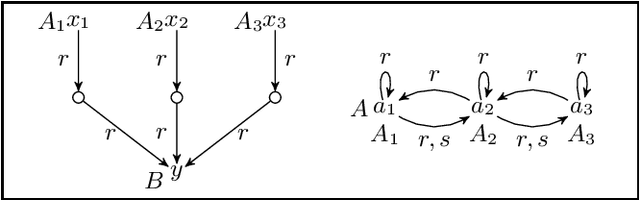
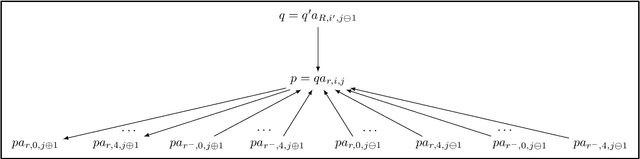
We introduce and study several notions of approximation for ontology-mediated queries based on the description logics ALC and ALCI. Our approximations are of two kinds: we may (1) replace the ontology with one formulated in a tractable ontology language such as ELI or certain TGDs and (2) replace the database with one from a tractable class such as the class of databases whose treewidth is bounded by a constant. We determine the computational complexity and the relative completeness of the resulting approximations. (Almost) all of them reduce the data complexity from coNP-complete to PTime, in some cases even to fixed-parameter tractable and to linear time. While approximations of kind (1) also reduce the combined complexity, this tends to not be the case for approximations of kind (2). In some cases, the combined complexity even increases.

A Journey into Ontology Approximation: From Non-Horn to Hon

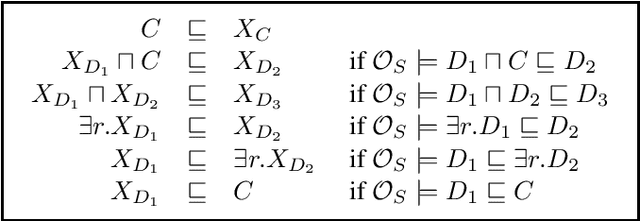
We study complete approximations of an ontology formulated in a non-Horn description logic (DL) such as $\mathcal{ALC}$ in a Horn DL such as~$\mathcal{EL}$. We provide concrete approximation schemes that are necessarily infinite and observe that in the $\mathcal{ELU}$-to-$\mathcal{EL}$ case finite approximations tend to exist in practice and are guaranteed to exist when the original ontology is acyclic. In contrast, neither of this is the case for $\mathcal{ELU}_\bot$-to-$\mathcal{EL}_\bot$ and for $\mathcal{ALC}$-to-$\mathcal{EL}_\bot$ approximations. We also define a notion of approximation tailored towards ontology-mediated querying, connect it to subsumption-based approximations, and identify a case where finite approximations are guaranteed to exist.