A Journey into Ontology Approximation: From Non-Horn to Hon
Paper and Code
Jan 25, 2020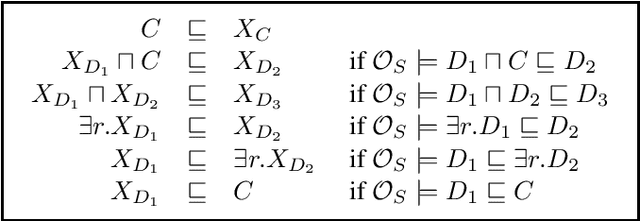
We study complete approximations of an ontology formulated in a non-Horn description logic (DL) such as $\mathcal{ALC}$ in a Horn DL such as~$\mathcal{EL}$. We provide concrete approximation schemes that are necessarily infinite and observe that in the $\mathcal{ELU}$-to-$\mathcal{EL}$ case finite approximations tend to exist in practice and are guaranteed to exist when the original ontology is acyclic. In contrast, neither of this is the case for $\mathcal{ELU}_\bot$-to-$\mathcal{EL}_\bot$ and for $\mathcal{ALC}$-to-$\mathcal{EL}_\bot$ approximations. We also define a notion of approximation tailored towards ontology-mediated querying, connect it to subsumption-based approximations, and identify a case where finite approximations are guaranteed to exist.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge