Query Expressibility and Verification in Ontology-Based Data Access

In ontology-based data access, multiple data sources are integrated using an ontology and mappings. In practice, this is often achieved by a bootstrapping process, that is, the ontology and mappings are first designed to support only the most important queries over the sources and then gradually extended to enable additional queries. In this paper, we study two reasoning problems that support such an approach. The expressibility problem asks whether a given source query $q_s$ is expressible as a target query (that is, over the ontology's vocabulary) and the verification problem asks, additionally given a candidate target query $q_t$, whether $q_t$ expresses $q_s$. We consider (U)CQs as source and target queries and GAV mappings, showing that both problems are $\Pi^p_2$-complete in DL-Lite, coNExpTime-complete between EL and ELHI when source queries are rooted, and 2ExpTime-complete for unrestricted source queries.

A Journey into Ontology Approximation: From Non-Horn to Hon

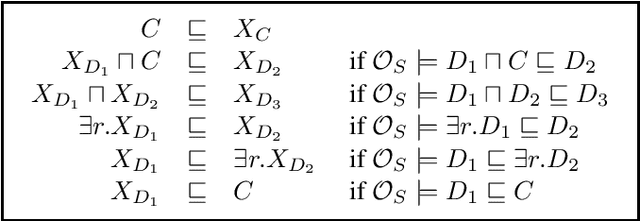
We study complete approximations of an ontology formulated in a non-Horn description logic (DL) such as $\mathcal{ALC}$ in a Horn DL such as~$\mathcal{EL}$. We provide concrete approximation schemes that are necessarily infinite and observe that in the $\mathcal{ELU}$-to-$\mathcal{EL}$ case finite approximations tend to exist in practice and are guaranteed to exist when the original ontology is acyclic. In contrast, neither of this is the case for $\mathcal{ELU}_\bot$-to-$\mathcal{EL}_\bot$ and for $\mathcal{ALC}$-to-$\mathcal{EL}_\bot$ approximations. We also define a notion of approximation tailored towards ontology-mediated querying, connect it to subsumption-based approximations, and identify a case where finite approximations are guaranteed to exist.