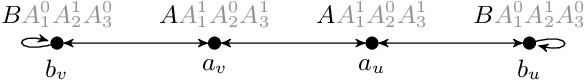
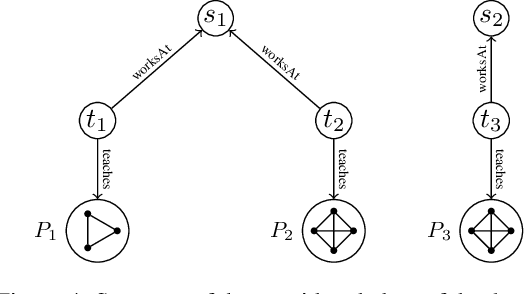
Description Logics with Abstraction and Refinement

Ontologies often require knowledge representation on multiple levels of abstraction, but description logics (DLs) are not well-equipped for supporting this. We propose an extension of DLs in which abstraction levels are first-class citizens and which provides explicit operators for the abstraction and refinement of concepts and roles across multiple abstraction levels, based on conjunctive queries. We prove that reasoning in the resulting family of DLs is decidable while several seemingly harmless variations turn out to be undecidable. We also pinpoint the precise complexity of our logics and several relevant fragments.

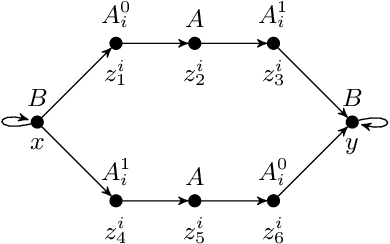
Ontology-Mediated Querying on Databases of Bounded Cliquewidth

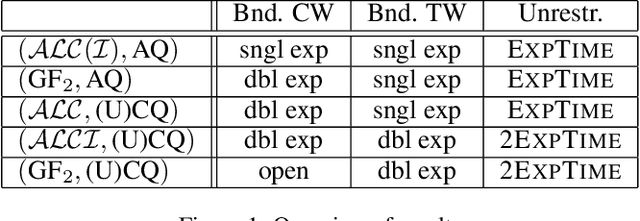
We study the evaluation of ontology-mediated queries (OMQs) on databases of bounded cliquewidth from the viewpoint of parameterized complexity theory. As the ontology language, we consider the description logics $\mathcal{ALC}$ and $\mathcal{ALCI}$ as well as the guarded two-variable fragment GF$_2$ of first-order logic. Queries are atomic queries (AQs), conjunctive queries (CQs), and unions of CQs. All studied OMQ problems are fixed-parameter linear (FPL) when the parameter is the size of the OMQ plus the cliquewidth. Our main contribution is a detailed analysis of the dependence of the running time on the parameter, exhibiting several interesting effects.