Reverse Engineering of Temporal Queries Mediated by LTL Ontologies

In reverse engineering of database queries, we aim to construct a query from a given set of answers and non-answers; it can then be used to explore the data further or as an explanation of the answers and non-answers. We investigate this query-by-example problem for queries formulated in positive fragments of linear temporal logic LTL over timestamped data, focusing on the design of suitable query languages and the combined and data complexity of deciding whether there exists a query in the given language that separates the given answers from non-answers. We consider both plain LTL queries and those mediated by LTL-ontologies.

Inseparability and Conservative Extensions of Description Logic Ontologies: A Survey

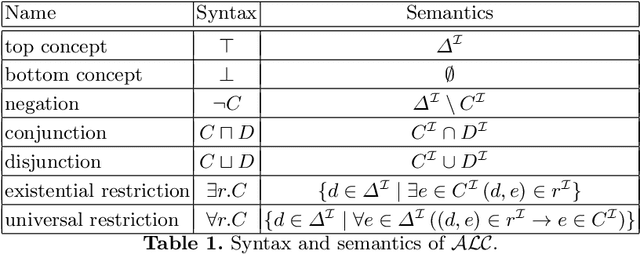
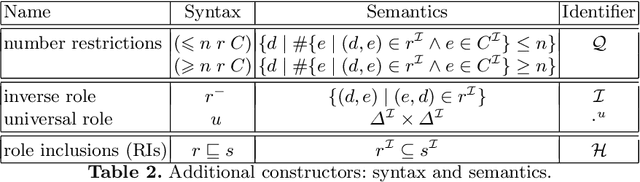
The question whether an ontology can safely be replaced by another, possibly simpler, one is fundamental for many ontology engineering and maintenance tasks. It underpins, for example, ontology versioning, ontology modularization, forgetting, and knowledge exchange. What safe replacement means depends on the intended application of the ontology. If, for example, it is used to query data, then the answers to any relevant ontology-mediated query should be the same over any relevant data set; if, in contrast, the ontology is used for conceptual reasoning, then the entailed subsumptions between concept expressions should coincide. This gives rise to different notions of ontology inseparability such as query inseparability and concept inseparability, which generalize corresponding notions of conservative extensions. We survey results on various notions of inseparability in the context of description logic ontologies, discussing their applications, useful model-theoretic characterizations, algorithms for determining whether two ontologies are inseparable (and, sometimes, for computing the difference between them if they are not), and the computational complexity of this problem.

Exact Learning of Lightweight Description Logic Ontologies

We study the problem of learning description logic (DL) ontologies in Angluin et al.'s framework of exact learning via queries. We admit membership queries ("is a given subsumption entailed by the target ontology?") and equivalence queries ("is a given ontology equivalent to the target ontology?"). We present three main results: (1) ontologies formulated in (two relevant versions of) the description logic DL-Lite can be learned with polynomially many queries of polynomial size; (2) this is not the case for ontologies formulated in the description logic EL, even when only acyclic ontologies are admitted; and (3) ontologies formulated in a fragment of EL related to the web ontology language OWL 2 RL can be learned in polynomial time. We also show that neither membership nor equivalence queries alone are sufficient in cases (1) and (3).

The Logical Difference for the Lightweight Description Logic EL

We study a logic-based approach to versioning of ontologies. Under this view, ontologies provide answers to queries about some vocabulary of interest. The difference between two versions of an ontology is given by the set of queries that receive different answers. We investigate this approach for terminologies given in the description logic EL extended with role inclusions and domain and range restrictions for three distinct types of queries: subsumption, instance, and conjunctive queries. In all three cases, we present polynomial-time algorithms that decide whether two terminologies give the same answers to queries over a given vocabulary and compute a succinct representation of the difference if it is non- empty. We present an implementation, CEX2, of the developed algorithms for subsumption and instance queries and apply it to distinct versions of Snomed CT and the NCI ontology.