Ontology-Mediated Queries: Combined Complexity and Succinctness of Rewritings via Circuit Complexity

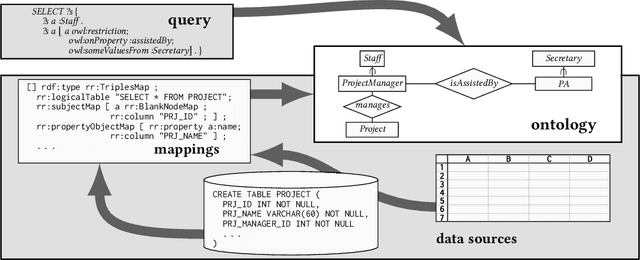
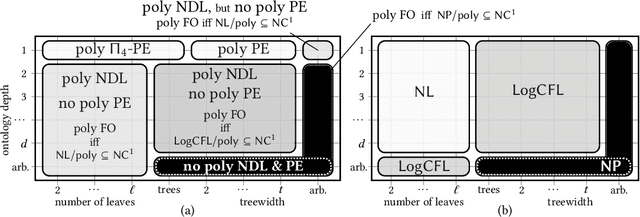
We give solutions to two fundamental computational problems in ontology-based data access with the W3C standard ontology language OWL 2 QL: the succinctness problem for first-order rewritings of ontology-mediated queries (OMQs), and the complexity problem for OMQ answering. We classify OMQs according to the shape of their conjunctive queries (treewidth, the number of leaves) and the existential depth of their ontologies. For each of these classes, we determine the combined complexity of OMQ answering, and whether all OMQs in the class have polynomial-size first-order, positive existential, and nonrecursive datalog rewritings. We obtain the succinctness results using hypergraph programs, a new computational model for Boolean functions, which makes it possible to connect the size of OMQ rewritings and circuit complexity.

A Cookbook for Temporal Conceptual Data Modelling with Description Logics

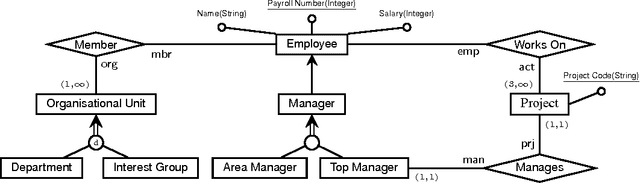
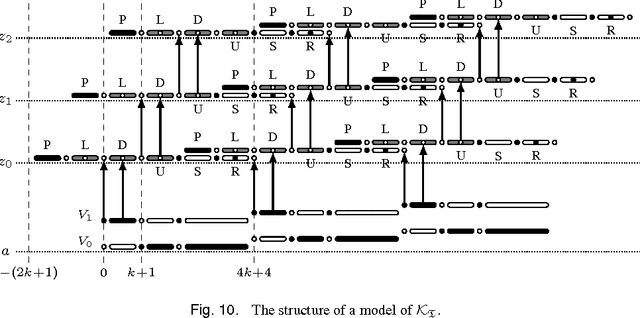
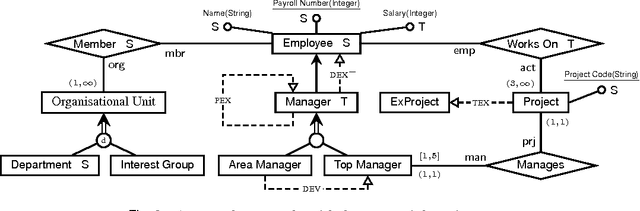
We design temporal description logics suitable for reasoning about temporal conceptual data models and investigate their computational complexity. Our formalisms are based on DL-Lite logics with three types of concept inclusions (ranging from atomic concept inclusions and disjointness to the full Booleans), as well as cardinality constraints and role inclusions. In the temporal dimension, they capture future and past temporal operators on concepts, flexible and rigid roles, the operators `always' and `some time' on roles, data assertions for particular moments of time and global concept inclusions. The logics are interpreted over the Cartesian products of object domains and the flow of time (Z,<), satisfying the constant domain assumption. We prove that the most expressive of our temporal description logics (which can capture lifespan cardinalities and either qualitative or quantitative evolution constraints) turn out to be undecidable. However, by omitting some of the temporal operators on concepts/roles or by restricting the form of concept inclusions we obtain logics whose complexity ranges between PSpace and NLogSpace. These positive results were obtained by reduction to various clausal fragments of propositional temporal logic, which opens a way to employ propositional or first-order temporal provers for reasoning about temporal data models.

The DL-Lite Family and Relations

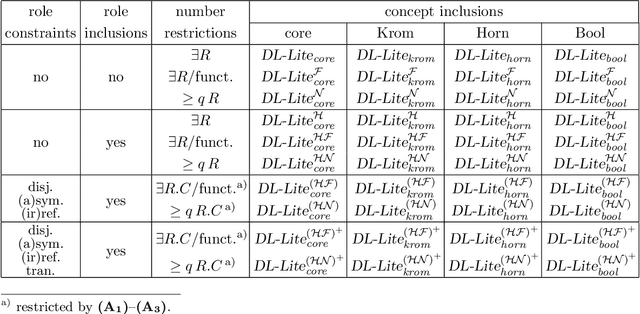
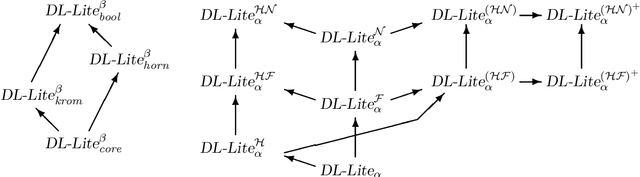
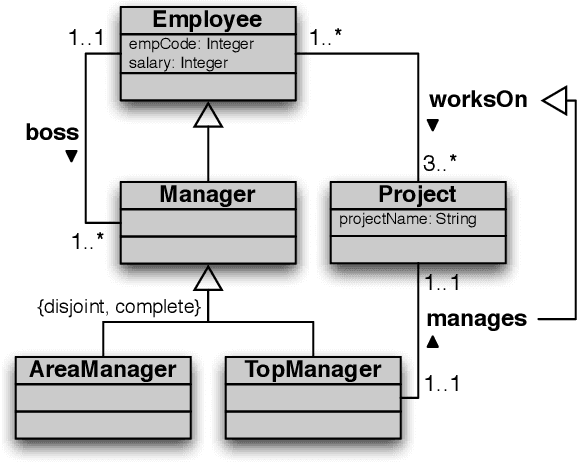
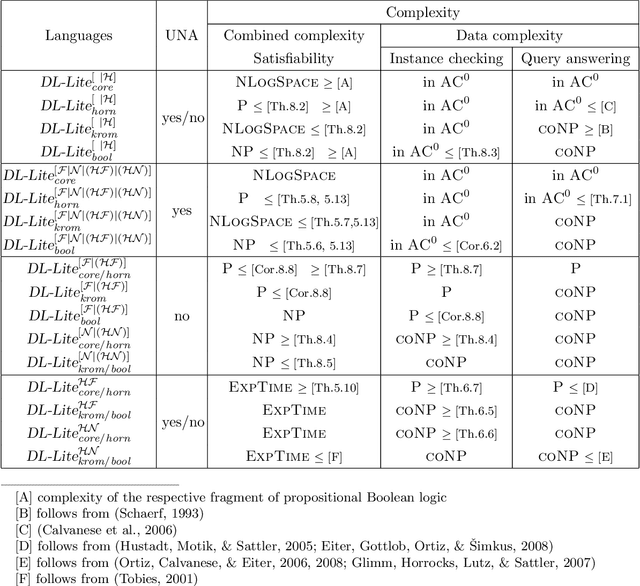
The recently introduced series of description logics under the common moniker DL-Lite has attracted attention of the description logic and semantic web communities due to the low computational complexity of inference, on the one hand, and the ability to represent conceptual modeling formalisms, on the other. The main aim of this article is to carry out a thorough and systematic investigation of inference in extensions of the original DL-Lite logics along five axes: by (i) adding the Boolean connectives and (ii) number restrictions to concept constructs, (iii) allowing role hierarchies, (iv) allowing role disjointness, symmetry, asymmetry, reflexivity, irreflexivity and transitivity constraints, and (v) adopting or dropping the unique same assumption. We analyze the combined complexity of satisfiability for the resulting logics, as well as the data complexity of instance checking and answering positive existential queries. Our approach is based on embedding DL-Lite logics in suitable fragments of the one-variable first-order logic, which provides useful insights into their properties and, in particular, computational behavior.

Temporal Description Logic for Ontology-Based Data Access (Extended Version)

Our aim is to investigate ontology-based data access over temporal data with validity time and ontologies capable of temporal conceptual modelling. To this end, we design a temporal description logic, TQL, that extends the standard ontology language OWL 2 QL, provides basic means for temporal conceptual modelling and ensures first-order rewritability of conjunctive queries for suitably defined data instances with validity time.