Hadrien Pulcini
Separating Positive and Negative Data Examples by Concepts and Formulas: The Case of Restricted Signatures
Jul 06, 2020Abstract:We study the separation of positive and negative data examples in terms of description logic (DL) concepts and formulas of decidable FO fragments, in the presence of an ontology. In contrast to previous work, we add a signature that specifies a subset of the symbols from the data and ontology that can be used for separation. We consider weak and strong versions of the resulting problem that differ in how the negative examples are treated. Our main results are that (a projective form of) the weak version is decidable in $\mathcal{ALCI}$ while it is undecidable in the guarded fragment GF, the guarded negation fragment GNF, and the DL $\mathcal{ALCFIO}$, and that strong separability is decidable in $\mathcal{ALCI}$, GF, and GNF. We also provide (mostly tight) complexity bounds.
Logical Separability of Incomplete Data under Ontologies
Jul 03, 2020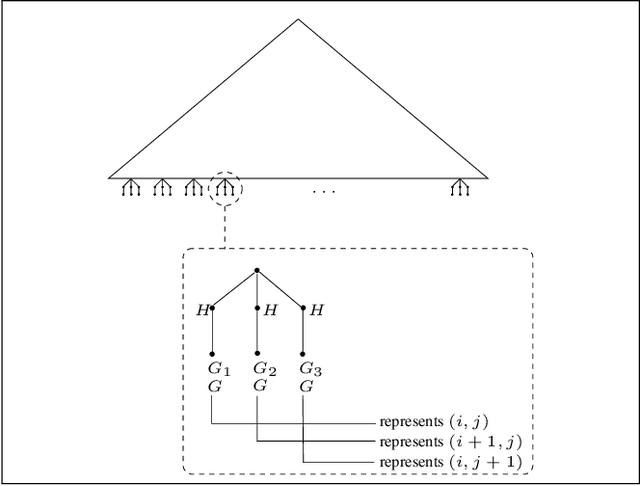
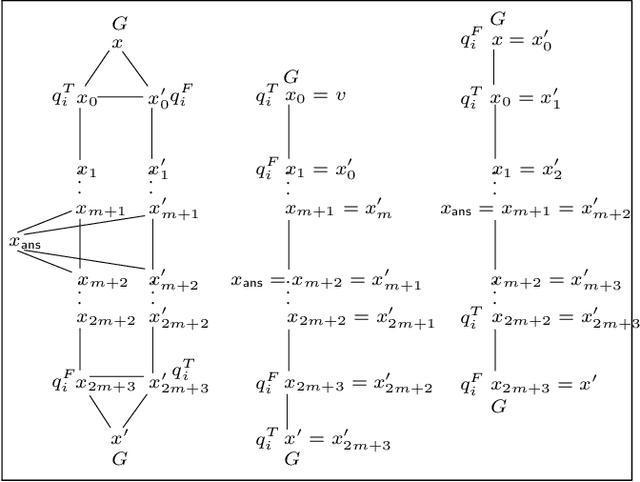
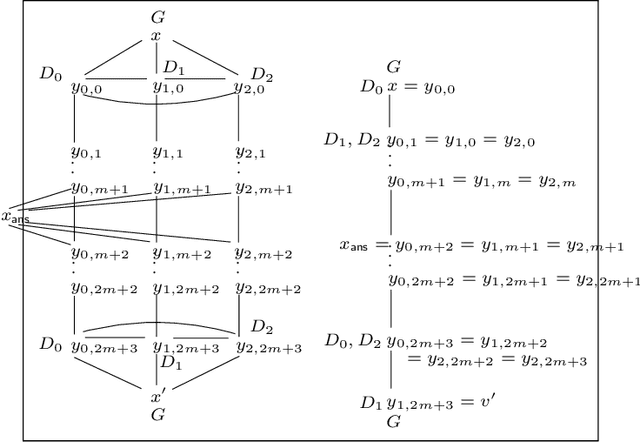
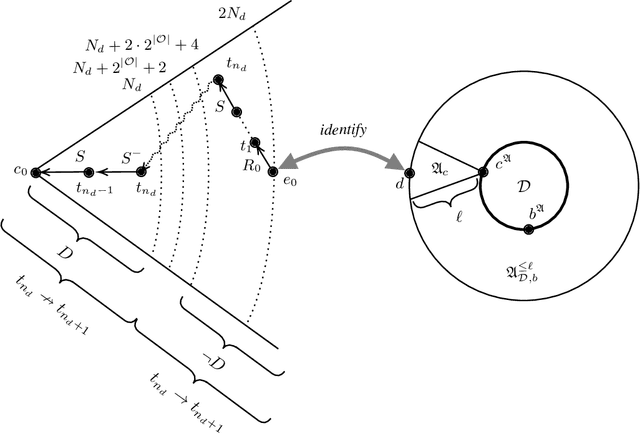
Abstract:Finding a logical formula that separates positive and negative examples given in the form of labeled data items is fundamental in applications such as concept learning, reverse engineering of database queries, and generating referring expressions. In this paper, we investigate the existence of a separating formula for incomplete data in the presence of an ontology. Both for the ontology language and the separation language, we concentrate on first-order logic and three important fragments thereof: the description logic $\mathcal{ALCI}$, the guarded fragment, and the two-variable fragment. We consider several forms of separability that differ in the treatment of negative examples and in whether or not they admit the use of additional helper symbols to achieve separation. We characterize separability in a model-theoretic way, compare the separating power of the different languages, and determine the computational complexity of separability as a decision problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge