Abstract Modular Systems and Solvers

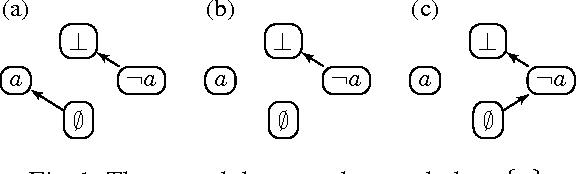
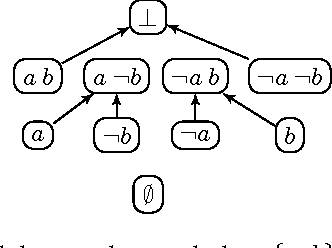
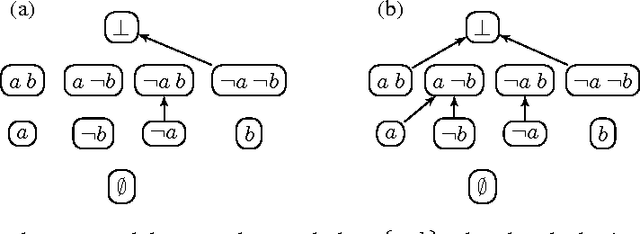
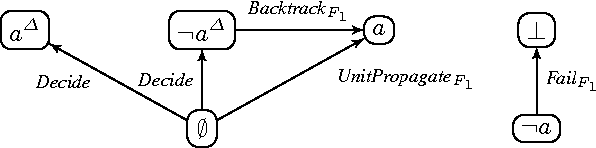
Integrating diverse formalisms into modular knowledge representation systems offers increased expressivity, modeling convenience and computational benefits. We introduce concepts of abstract modules and abstract modular systems to study general principles behind the design and analysis of model-finding programs, or solvers, for integrated heterogeneous multi-logic systems. We show how abstract modules and abstract modular systems give rise to transition systems, which are a natural and convenient representation of solvers pioneered by the SAT community. We illustrate our approach by showing how it applies to answer set programming and propositional logic, and to multi-logic systems based on these two formalisms.