Origins of Answer-Set Programming - Some Background And Two Personal Accounts

We discuss the evolution of aspects of nonmonotonic reasoning towards the computational paradigm of answer-set programming (ASP). We give a general overview of the roots of ASP and follow up with the personal perspective on research developments that helped verbalize the main principles of ASP and differentiated it from the classical logic programming.

Reiter's Default Logic Is a Logic of Autoepistemic Reasoning And a Good One, Too

A fact apparently not observed earlier in the literature of nonmonotonic reasoning is that Reiter, in his default logic paper, did not directly formalize informal defaults. Instead, he translated a default into a certain natural language proposition and provided a formalization of the latter. A few years later, Moore noted that propositions like the one used by Reiter are fundamentally different than defaults and exhibit a certain autoepistemic nature. Thus, Reiter had developed his default logic as a formalization of autoepistemic propositions rather than of defaults. The first goal of this paper is to show that some problems of Reiter's default logic as a formal way to reason about informal defaults are directly attributable to the autoepistemic nature of default logic and to the mismatch between informal defaults and the Reiter's formal defaults, the latter being a formal expression of the autoepistemic propositions Reiter used as a representation of informal defaults. The second goal of our paper is to compare the work of Reiter and Moore. While each of them attempted to formalize autoepistemic propositions, the modes of reasoning in their respective logics were different. We revisit Moore's and Reiter's intuitions and present them from the perspective of autotheoremhood, where theories can include propositions referring to the theory's own theorems. We then discuss the formalization of this perspective in the logics of Moore and Reiter, respectively, using the unifying semantic framework for default and autoepistemic logics that we developed earlier. We argue that Reiter's default logic is a better formalization of Moore's intuitions about autoepistemic propositions than Moore's own autoepistemic logic.

On the Expressibility of Stable Logic Programming

(We apologize for pidgin LaTeX) Schlipf \cite{sch91} proved that Stable Logic Programming (SLP) solves all $\mathit{NP}$ decision problems. We extend Schlipf's result to prove that SLP solves all search problems in the class $\mathit{NP}$. Moreover, we do this in a uniform way as defined in \cite{mt99}. Specifically, we show that there is a single $\mathrm{DATALOG}^{\neg}$ program $P_{\mathit{Trg}}$ such that given any Turing machine $M$, any polynomial $p$ with non-negative integer coefficients and any input $\sigma$ of size $n$ over a fixed alphabet $\Sigma$, there is an extensional database $\mathit{edb}_{M,p,\sigma}$ such that there is a one-to-one correspondence between the stable models of $\mathit{edb}_{M,p,\sigma} \cup P_{\mathit{Trg}}$ and the accepting computations of the machine $M$ that reach the final state in at most $p(n)$ steps. Moreover, $\mathit{edb}_{M,p,\sigma}$ can be computed in polynomial time from $p$, $\sigma$ and the description of $M$ and the decoding of such accepting computations from its corresponding stable model of $\mathit{edb}_{M,p,\sigma} \cup P_{\mathit{Trg}}$ can be computed in linear time. A similar statement holds for Default Logic with respect to $\Sigma_2^\mathrm{P}$-search problems\footnote{The proof of this result involves additional technical complications and will be a subject of another publication.}.

Ultimate approximations in nonmonotonic knowledge representation systems

We study fixpoints of operators on lattices. To this end we introduce the notion of an approximation of an operator. We order approximations by means of a precision ordering. We show that each lattice operator O has a unique most precise or ultimate approximation. We demonstrate that fixpoints of this ultimate approximation provide useful insights into fixpoints of the operator O. We apply our theory to logic programming and introduce the ultimate Kripke-Kleene, well-founded and stable semantics. We show that the ultimate Kripke-Kleene and well-founded semantics are more precise then their standard counterparts We argue that ultimate semantics for logic programming have attractive epistemological properties and that, while in general they are computationally more complex than the standard semantics, for many classes of theories, their complexity is no worse.

Uniform semantic treatment of default and autoepistemic logics

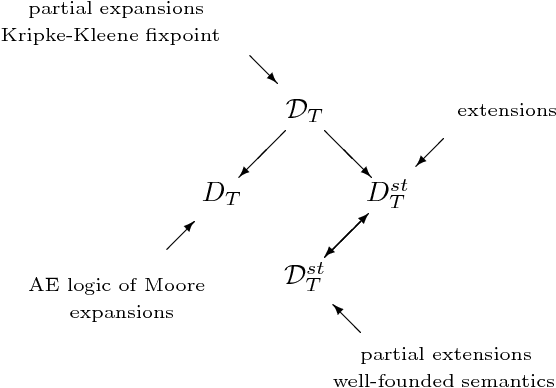
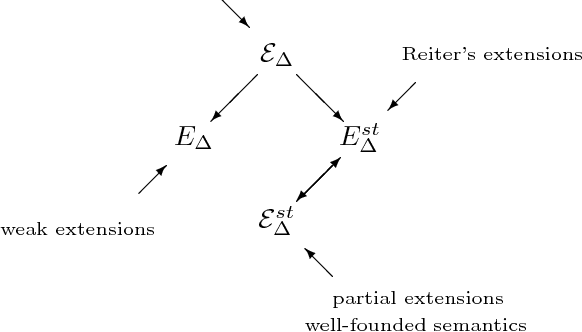
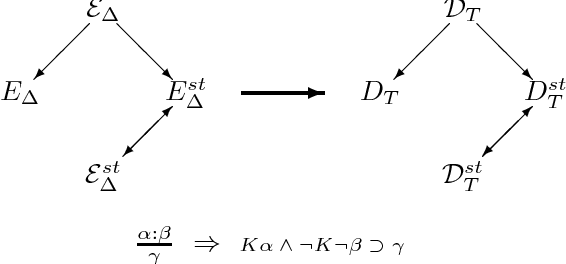
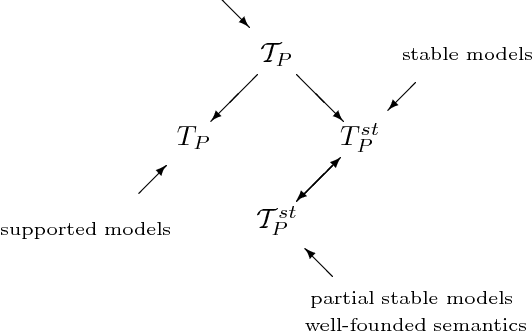
We revisit the issue of connections between two leading formalisms in nonmonotonic reasoning: autoepistemic logic and default logic. For each logic we develop a comprehensive semantic framework based on the notion of a belief pair. The set of all belief pairs together with the so called knowledge ordering forms a complete lattice. For each logic, we introduce several semantics by means of fixpoints of operators on the lattice of belief pairs. Our results elucidate an underlying isomorphism of the respective semantic constructions. In particular, we show that the interpretation of defaults as modal formulas proposed by Konolige allows us to represent all semantics for default logic in terms of the corresponding semantics for autoepistemic logic. Thus, our results conclusively establish that default logic can indeed be viewed as a fragment of autoepistemic logic. However, as we also demonstrate, the semantics of Moore and Reiter are given by different operators and occupy different locations in their corresponding families of semantics. This result explains the source of the longstanding difficulty to formally relate these two semantics. In the paper, we also discuss approximating skeptical reasoning with autoepistemic and default logics and establish constructive principles behind such approximations.

Stable models and an alternative logic programming paradigm

In this paper we reexamine the place and role of stable model semantics in logic programming and contrast it with a least Herbrand model approach to Horn programs. We demonstrate that inherent features of stable model semantics naturally lead to a logic programming system that offers an interesting alternative to more traditional logic programming styles of Horn logic programming, stratified logic programming and logic programming with well-founded semantics. The proposed approach is based on the interpretation of program clauses as constraints. In this setting programs do not describe a single intended model, but a family of stable models. These stable models encode solutions to the constraint satisfaction problem described by the program. Our approach imposes restrictions on the syntax of logic programs. In particular, function symbols are eliminated from the language. We argue that the resulting logic programming system is well-attuned to problems in the class NP, has a well-defined domain of applications, and an emerging methodology of programming. We point out that what makes the whole approach viable is recent progress in implementations of algorithms to compute stable models of propositional logic programs.