Uniform semantic treatment of default and autoepistemic logics

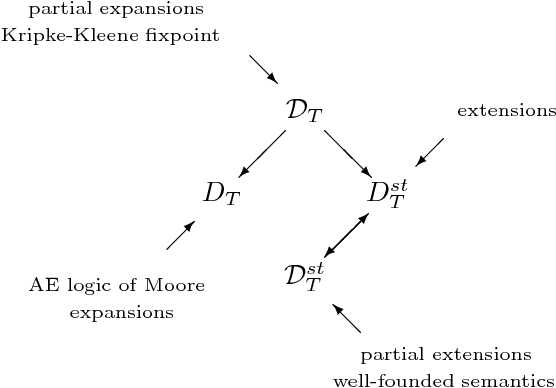
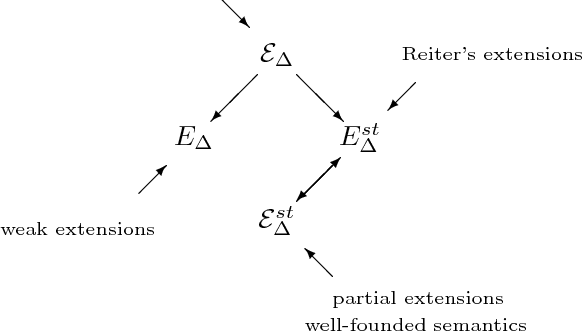
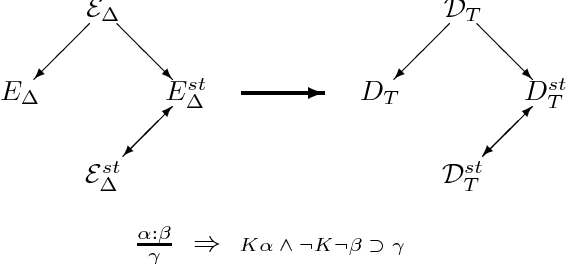
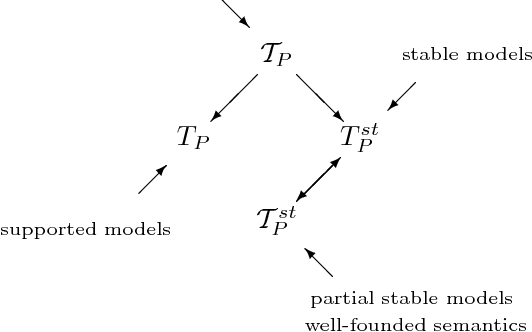
We revisit the issue of connections between two leading formalisms in nonmonotonic reasoning: autoepistemic logic and default logic. For each logic we develop a comprehensive semantic framework based on the notion of a belief pair. The set of all belief pairs together with the so called knowledge ordering forms a complete lattice. For each logic, we introduce several semantics by means of fixpoints of operators on the lattice of belief pairs. Our results elucidate an underlying isomorphism of the respective semantic constructions. In particular, we show that the interpretation of defaults as modal formulas proposed by Konolige allows us to represent all semantics for default logic in terms of the corresponding semantics for autoepistemic logic. Thus, our results conclusively establish that default logic can indeed be viewed as a fragment of autoepistemic logic. However, as we also demonstrate, the semantics of Moore and Reiter are given by different operators and occupy different locations in their corresponding families of semantics. This result explains the source of the longstanding difficulty to formally relate these two semantics. In the paper, we also discuss approximating skeptical reasoning with autoepistemic and default logics and establish constructive principles behind such approximations.