Safe Reinforcement Learning via Probabilistic Logic Shields

Safe Reinforcement learning (Safe RL) aims at learning optimal policies while staying safe. A popular solution to Safe RL is shielding, which uses a logical safety specification to prevent an RL agent from taking unsafe actions. However, traditional shielding techniques are difficult to integrate with continuous, end-to-end deep RL methods. To this end, we introduce Probabilistic Logic Policy Gradient (PLPG). PLPG is a model-based Safe RL technique that uses probabilistic logic programming to model logical safety constraints as differentiable functions. Therefore, PLPG can be seamlessly applied to any policy gradient algorithm while still providing the same convergence guarantees. In our experiments, we show that PLPG learns safer and more rewarding policies compared to other state-of-the-art shielding techniques.

Learning Probabilistic Temporal Safety Properties from Examples in Relational Domains

We propose a framework for learning a fragment of probabilistic computation tree logic (pCTL) formulae from a set of states that are labeled as safe or unsafe. We work in a relational setting and combine ideas from relational Markov Decision Processes with pCTL model-checking. More specifically, we assume that there is an unknown relational pCTL target formula that is satisfied by only safe states, and has a horizon of maximum $k$ steps and a threshold probability $\alpha$. The task then consists of learning this unknown formula from states that are labeled as safe or unsafe by a domain expert. We apply principles of relational learning to induce a pCTL formula that is satisfied by all safe states and none of the unsafe ones. This formula can then be used as a safety specification for this domain, so that the system can avoid getting into dangerous situations in future. Following relational learning principles, we introduce a candidate formula generation process, as well as a method for deciding which candidate formula is a satisfactory specification for the given labeled states. The cases where the expert knows and does not know the system policy are treated, however, much of the learning process is the same for both cases. We evaluate our approach on a synthetic relational domain.

Online Learning of Non-Markovian Reward Models

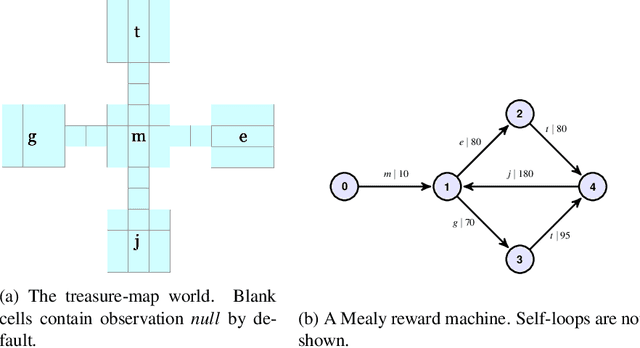
There are situations in which an agent should receive rewards only after having accomplished a series of previous tasks, that is, rewards are non-Markovian. One natural and quite general way to represent history-dependent rewards is via a Mealy machine, a finite state automaton that produces output sequences from input sequences. In our formal setting, we consider a Markov decision process (MDP) that models the dynamics of the environment in which the agent evolves and a Mealy machine synchronized with this MDP to formalize the non-Markovian reward function. While the MDP is known by the agent, the reward function is unknown to the agent and must be learned. Our approach to overcome this challenge is to use Angluin's $L^*$ active learning algorithm to learn a Mealy machine representing the underlying non-Markovian reward machine (MRM). Formal methods are used to determine the optimal strategy for answering so-called membership queries posed by $L^*$. Moreover, we prove that the expected reward achieved will eventually be at least as much as a given, reasonable value provided by a domain expert. We evaluate our framework on three problems. The results show that using $L^*$ to learn an MRM in a non-Markovian reward decision process is effective.

Reputation-driven Decision-making in Networks of Stochastic Agents

This paper studies multi-agent systems that involve networks of self-interested agents. We propose a Markov Decision Process-derived framework, called RepNet-MDP, tailored to domains in which agent reputation is a key driver of the interactions between agents. The fundamentals are based on the principles of RepNet-POMDP, a framework developed by Rens et al. in 2018, but addresses its mathematical inconsistencies and alleviates its intractability by only considering fully observable environments. We furthermore use an online learning algorithm for finding approximate solutions to RepNet-MDPs. In a series of experiments, RepNet agents are shown to be able to adapt their own behavior to the past behavior and reliability of the remaining agents of the network. Finally, our work identifies a limitation of the framework in its current formulation that prevents its agents from learning in circumstances in which they are not a primary actor.

Learning Non-Markovian Reward Models in MDPs

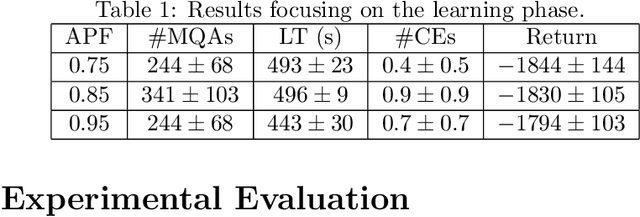
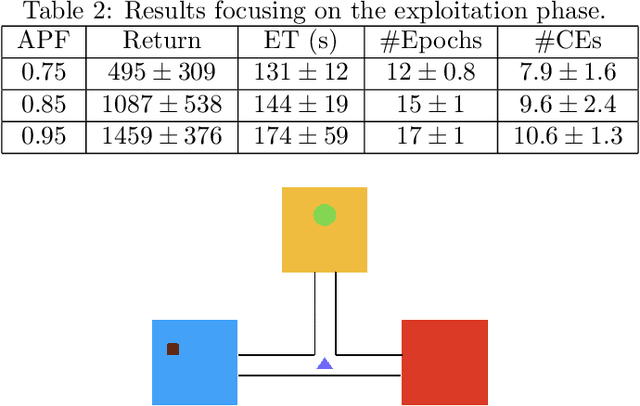
There are situations in which an agent should receive rewards only after having accomplished a series of previous tasks. In other words, the reward that the agent receives is non-Markovian. One natural and quite general way to represent history-dependent rewards is via a Mealy machine; a finite state automaton that produces output sequences (rewards in our case) from input sequences (state/action observations in our case). In our formal setting, we consider a Markov decision process (MDP) that models the dynamic of the environment in which the agent evolves and a Mealy machine synchronised with this MDP to formalise the non-Markovian reward function. While the MDP is known by the agent, the reward function is unknown from the agent and must be learnt. Learning non-Markov reward functions is a challenge. Our approach to overcome this challenging problem is a careful combination of the Angluin's L* active learning algorithm to learn finite automata, testing techniques for establishing conformance of finite model hypothesis and optimisation techniques for computing optimal strategies in Markovian (immediate) reward MDPs. We also show how our framework can be combined with classical heuristics such as Monte Carlo Tree Search. We illustrate our algorithms and a preliminary implementation on two typical examples for AI.

Maximizing Expected Impact in an Agent Reputation Network -- Technical Report

Many multi-agent systems (MASs) are situated in stochastic environments. Some such systems that are based on the partially observable Markov decision process (POMDP) do not take the benevolence of other agents for granted. We propose a new POMDP-based framework which is general enough for the specification of a variety of stochastic MAS domains involving the impact of agents on each other's reputations. A unique feature of this framework is that actions are specified as either undirected (regular) or directed (towards a particular agent), and a new directed transition function is provided for modeling the effects of reputation in interactions. Assuming that an agent must maintain a good enough reputation to survive in the network, a planning algorithm is developed for an agent to select optimal actions in stochastic MASs. Preliminary evaluation is provided via an example specification and by determining the algorithm's complexity.

Imagining Probabilistic Belief Change as Imaging (Technical Report)

Imaging is a form of probabilistic belief change which could be employed for both revision and update. In this paper, we propose a new framework for probabilistic belief change based on imaging, called Expected Distance Imaging (EDI). EDI is sufficiently general to define Bayesian conditioning and other forms of imaging previously defined in the literature. We argue that, and investigate how, EDI can be used for both revision and update. EDI's definition depends crucially on a weight function whose properties are studied and whose effect on belief change operations is analysed. Finally, four EDI instantiations are proposed, two for revision and two for update, and probabilistic rationality postulates are suggested for their analysis.

A Hybrid POMDP-BDI Agent Architecture with Online Stochastic Planning and Plan Caching

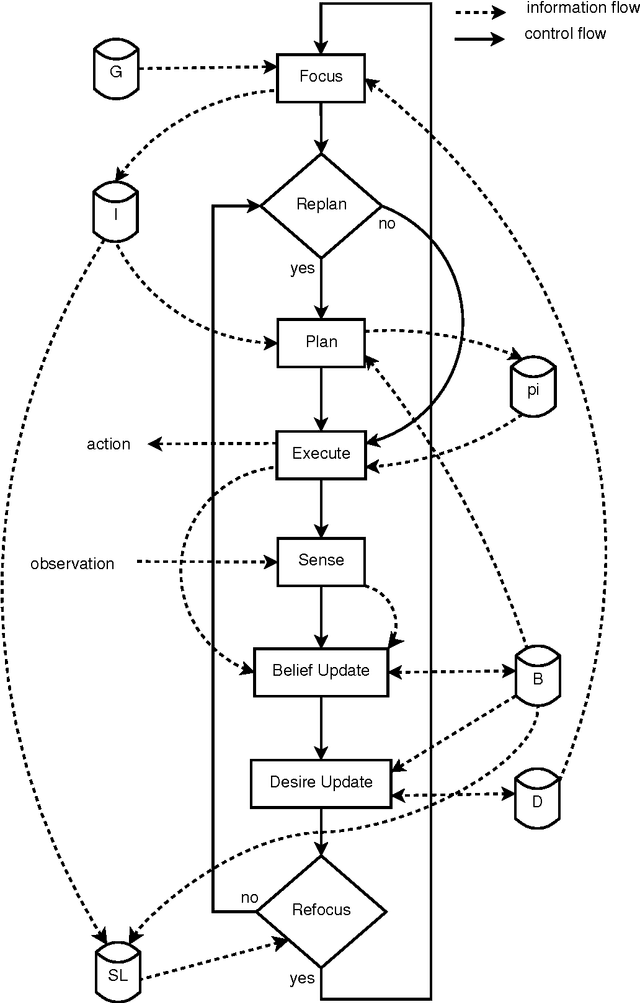
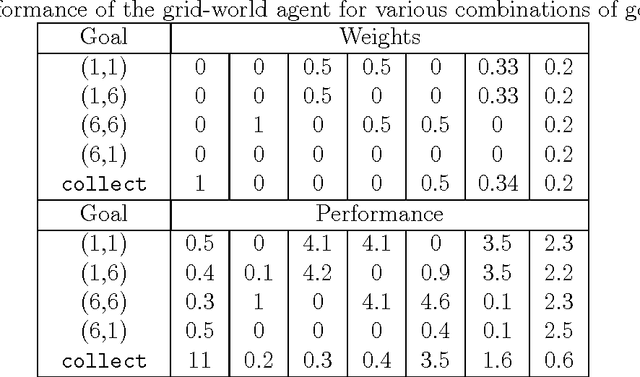
This article presents an agent architecture for controlling an autonomous agent in stochastic environments. The architecture combines the partially observable Markov decision process (POMDP) model with the belief-desire-intention (BDI) framework. The Hybrid POMDP-BDI agent architecture takes the best features from the two approaches, that is, the online generation of reward-maximizing courses of action from POMDP theory, and sophisticated multiple goal management from BDI theory. We introduce the advances made since the introduction of the basic architecture, including (i) the ability to pursue multiple goals simultaneously and (ii) a plan library for storing pre-written plans and for storing recently generated plans for future reuse. A version of the architecture without the plan library is implemented and is evaluated using simulations. The results of the simulation experiments indicate that the approach is feasible.

Revising Incompletely Specified Convex Probabilistic Belief Bases

We propose a method for an agent to revise its incomplete probabilistic beliefs when a new piece of propositional information is observed. In this work, an agent's beliefs are represented by a set of probabilistic formulae -- a belief base. The method involves determining a representative set of 'boundary' probability distributions consistent with the current belief base, revising each of these probability distributions and then translating the revised information into a new belief base. We use a version of Lewis Imaging as the revision operation. The correctness of the approach is proved. The expressivity of the belief bases under consideration are rather restricted, but has some applications. We also discuss methods of belief base revision employing the notion of optimum entropy, and point out some of the benefits and difficulties in those methods. Both the boundary distribution method and the optimum entropy method are reasonable, yet yield different results.

On Stochastic Belief Revision and Update and their Combination

I propose a framework for an agent to change its probabilistic beliefs when a new piece of propositional information $\alpha$ is observed. Traditionally, belief change occurs by either a revision process or by an update process, depending on whether the agent is informed with $\alpha$ in a static world or, respectively, whether $\alpha$ is a 'signal' from the environment due to an event occurring. Boutilier suggested a unified model of qualitative belief change, which "combines aspects of revision and update, providing a more realistic characterization of belief change." In this paper, I propose a unified model of quantitative belief change, where an agent's beliefs are represented as a probability distribution over possible worlds. As does Boutilier, I take a dynamical systems perspective. The proposed approach is evaluated against several rationality postulated, and some properties of the approach are worked out.