Raphaël Reynouad
Online Learning of Non-Markovian Reward Models
Sep 30, 2020
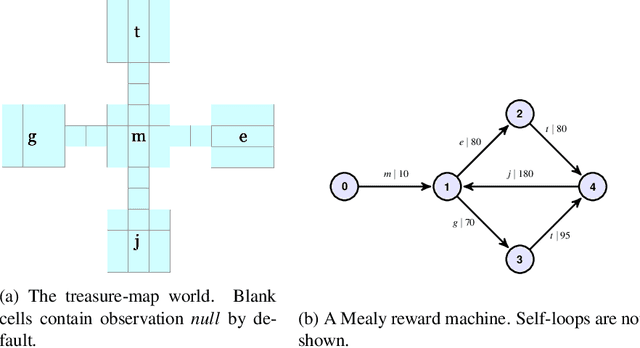


Abstract:There are situations in which an agent should receive rewards only after having accomplished a series of previous tasks, that is, rewards are non-Markovian. One natural and quite general way to represent history-dependent rewards is via a Mealy machine, a finite state automaton that produces output sequences from input sequences. In our formal setting, we consider a Markov decision process (MDP) that models the dynamics of the environment in which the agent evolves and a Mealy machine synchronized with this MDP to formalize the non-Markovian reward function. While the MDP is known by the agent, the reward function is unknown to the agent and must be learned. Our approach to overcome this challenge is to use Angluin's $L^*$ active learning algorithm to learn a Mealy machine representing the underlying non-Markovian reward machine (MRM). Formal methods are used to determine the optimal strategy for answering so-called membership queries posed by $L^*$. Moreover, we prove that the expected reward achieved will eventually be at least as much as a given, reasonable value provided by a domain expert. We evaluate our framework on three problems. The results show that using $L^*$ to learn an MRM in a non-Markovian reward decision process is effective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge