Learning Non-Markovian Reward Models in MDPs
Paper and Code
Jan 25, 2020
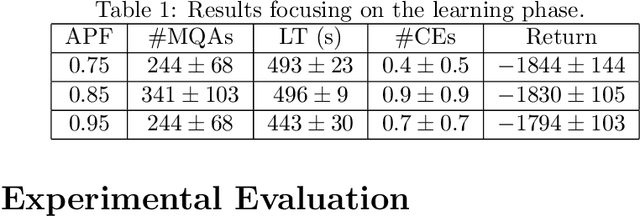

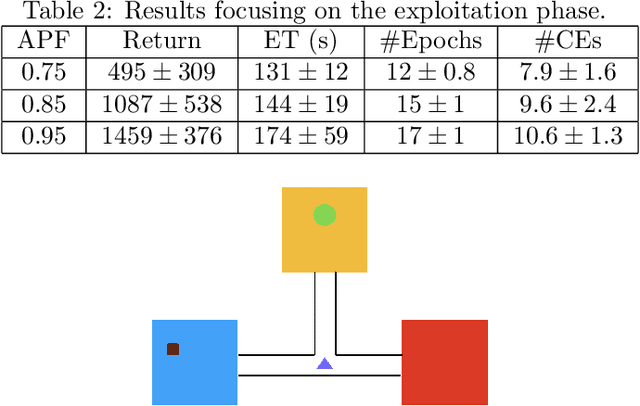
There are situations in which an agent should receive rewards only after having accomplished a series of previous tasks. In other words, the reward that the agent receives is non-Markovian. One natural and quite general way to represent history-dependent rewards is via a Mealy machine; a finite state automaton that produces output sequences (rewards in our case) from input sequences (state/action observations in our case). In our formal setting, we consider a Markov decision process (MDP) that models the dynamic of the environment in which the agent evolves and a Mealy machine synchronised with this MDP to formalise the non-Markovian reward function. While the MDP is known by the agent, the reward function is unknown from the agent and must be learnt. Learning non-Markov reward functions is a challenge. Our approach to overcome this challenging problem is a careful combination of the Angluin's L* active learning algorithm to learn finite automata, testing techniques for establishing conformance of finite model hypothesis and optimisation techniques for computing optimal strategies in Markovian (immediate) reward MDPs. We also show how our framework can be combined with classical heuristics such as Monte Carlo Tree Search. We illustrate our algorithms and a preliminary implementation on two typical examples for AI.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge