AdaNet: A Scalable and Flexible Framework for Automatically Learning Ensembles

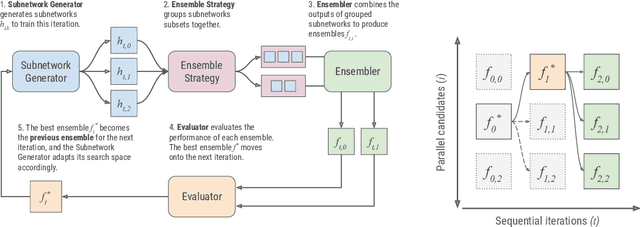
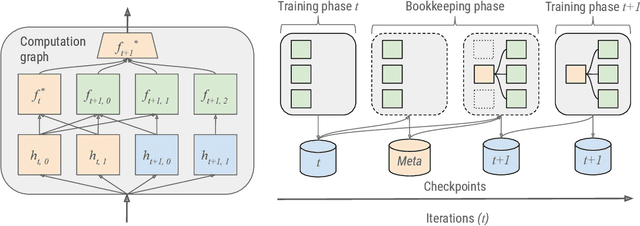
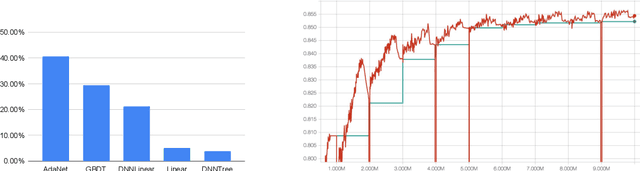
AdaNet is a lightweight TensorFlow-based (Abadi et al., 2015) framework for automatically learning high-quality ensembles with minimal expert intervention. Our framework is inspired by the AdaNet algorithm (Cortes et al., 2017) which learns the structure of a neural network as an ensemble of subnetworks. We designed it to: (1) integrate with the existing TensorFlow ecosystem, (2) offer sensible default search spaces to perform well on novel datasets, (3) present a flexible API to utilize expert information when available, and (4) efficiently accelerate training with distributed CPU, GPU, and TPU hardware. The code is open-source and available at: https://github.com/tensorflow/adanet.

Online Learning with Abstention

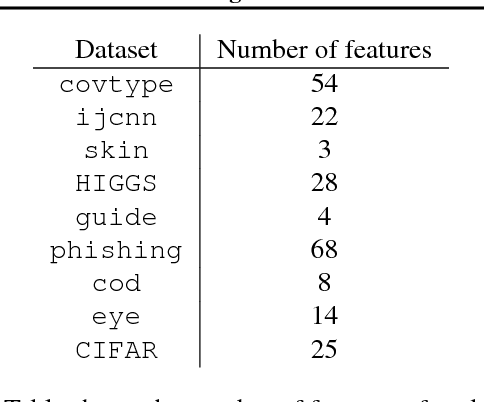
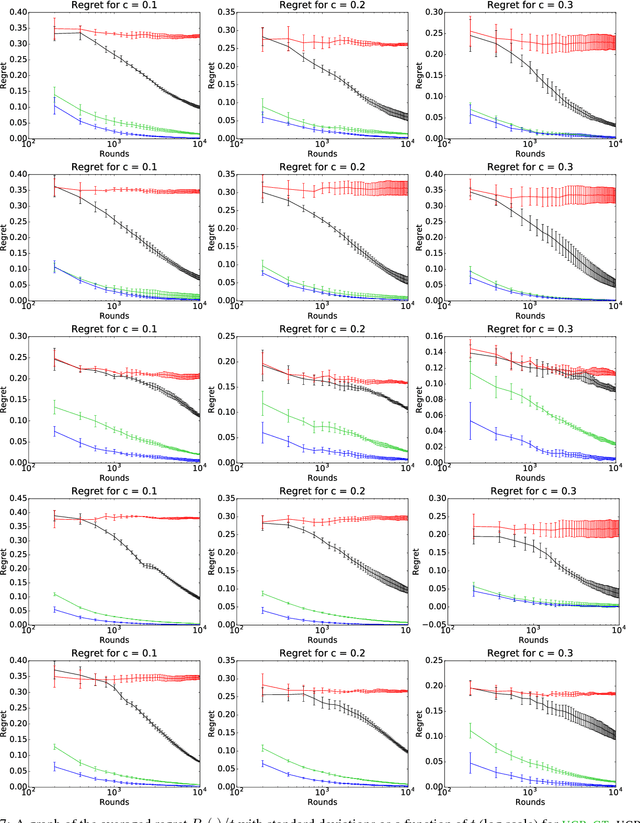
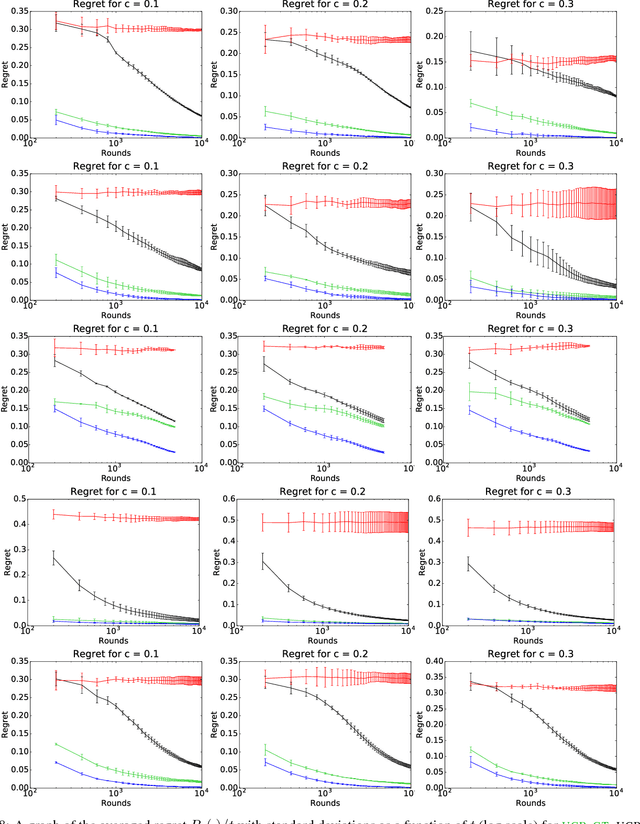
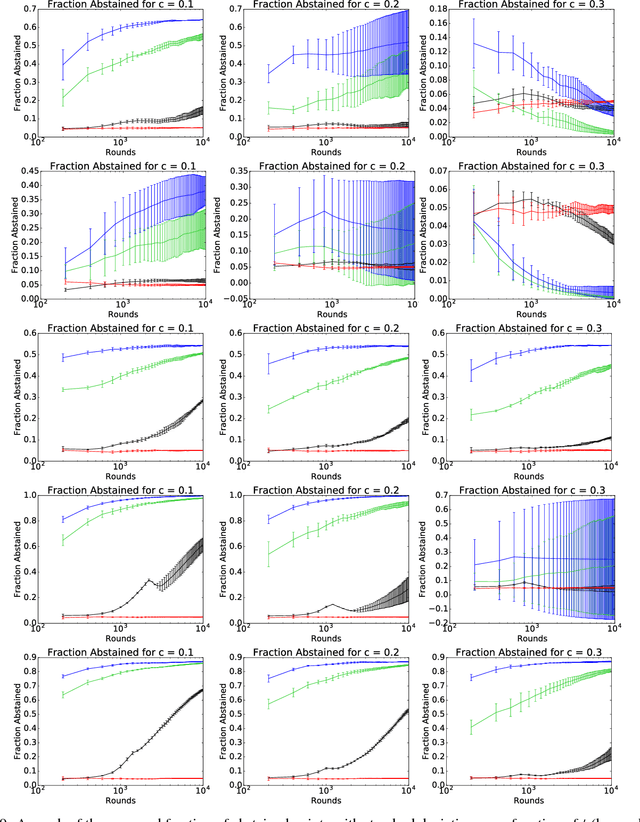
We present an extensive study of the key problem of online learning where algorithms are allowed to abstain from making predictions. In the adversarial setting, we show how existing online algorithms and guarantees can be adapted to this problem. In the stochastic setting, we first point out a bias problem that limits the straightforward extension of algorithms such as UCB-N to time-varying feedback graphs, as needed in this context. Next, we give a new algorithm, UCB-GT, that exploits historical data and is adapted to time-varying feedback graphs. We show that this algorithm benefits from more favorable regret guarantees than a possible, but limited, extension of UCB-N. We further report the results of a series of experiments demonstrating that UCB-GT largely outperforms that extension of UCB-N, as well as more standard baselines.

Discrepancy-Based Algorithms for Non-Stationary Rested Bandits

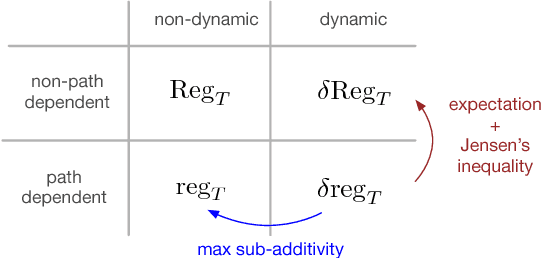
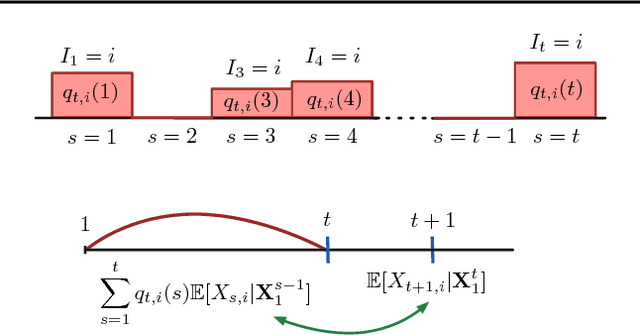
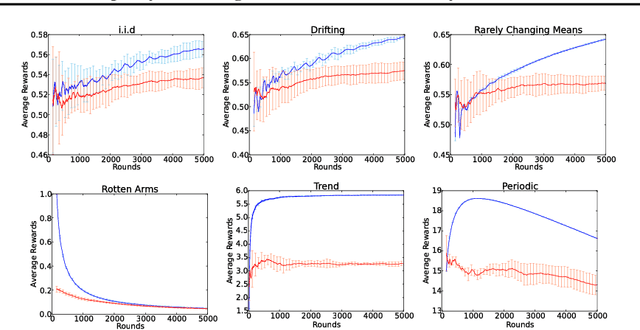
We study the multi-armed bandit problem where the rewards are realizations of general non-stationary stochastic processes, a setting that generalizes many existing lines of work and analyses. In particular, we present a theoretical analysis and derive regret guarantees for rested bandits in which the reward distribution of each arm changes only when we pull that arm. Remarkably, our regret bounds are logarithmic in the number of rounds under several natural conditions. We introduce a new algorithm based on classical UCB ideas combined with the notion of weighted discrepancy, a useful tool for measuring the non-stationarity of a stochastic process. We show that the notion of discrepancy can be used to design very general algorithms and a unified framework for the analysis of multi-armed rested bandit problems with non-stationary rewards. In particular, we show that we can recover the regret guarantees of many specific instances of bandit problems with non-stationary rewards that have been studied in the literature. We also provide experiments demonstrating that our algorithms can enjoy a significant improvement in practice compared to standard benchmarks.

Semi-automated Annotation of Signal Events in Clinical EEG Data

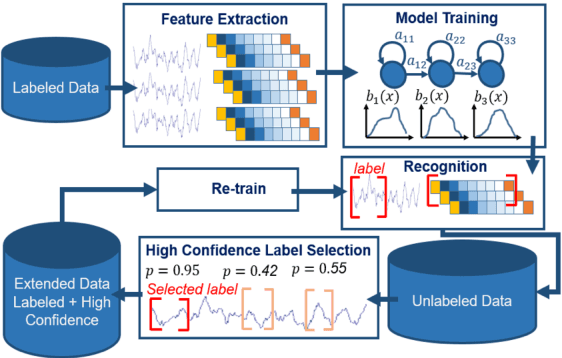
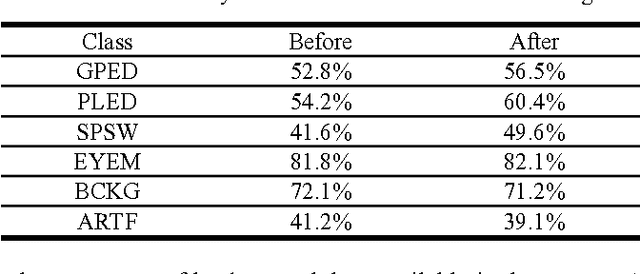
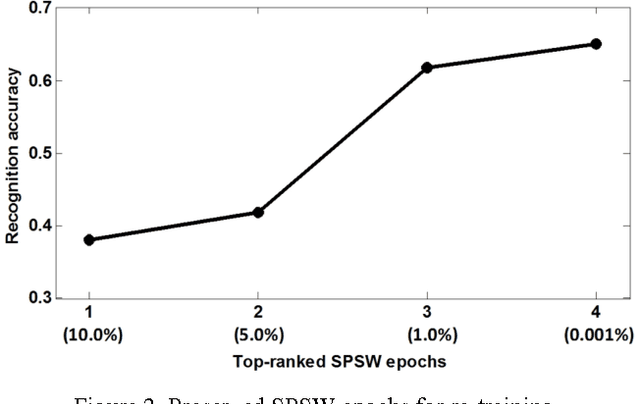
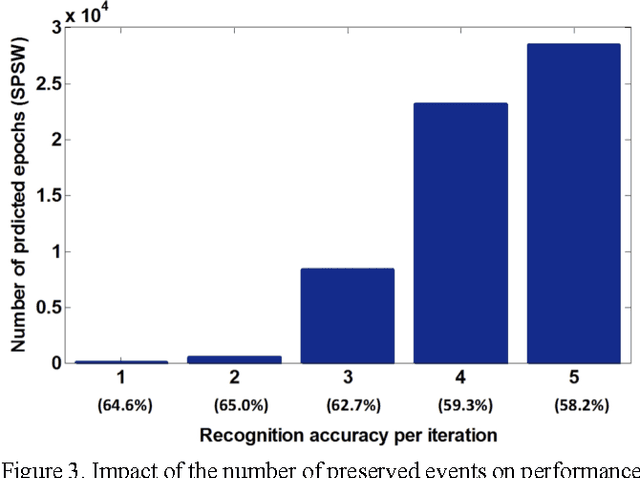
To be effective, state of the art machine learning technology needs large amounts of annotated data. There are numerous compelling applications in healthcare that can benefit from high performance automated decision support systems provided by deep learning technology, but they lack the comprehensive data resources required to apply sophisticated machine learning models. Further, for economic reasons, it is very difficult to justify the creation of large annotated corpora for these applications. Hence, automated annotation techniques become increasingly important. In this study, we investigated the effectiveness of using an active learning algorithm to automatically annotate a large EEG corpus. The algorithm is designed to annotate six types of EEG events. Two model training schemes, namely threshold-based and volume-based, are evaluated. In the threshold-based scheme the threshold of confidence scores is optimized in the initial training iteration, whereas for the volume-based scheme only a certain amount of data is preserved after each iteration. Recognition performance is improved 2% absolute and the system is capable of automatically annotating previously unlabeled data. Given that the interpretation of clinical EEG data is an exceedingly difficult task, this study provides some evidence that the proposed method is a viable alternative to expensive manual annotation.

An Analysis of Two Common Reference Points for EEGs

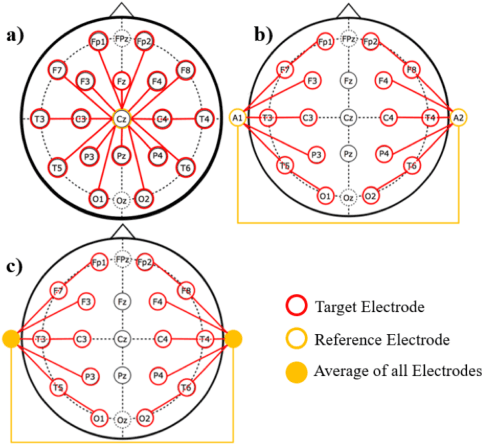
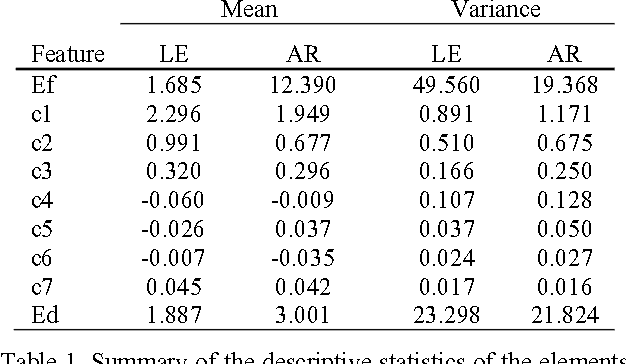
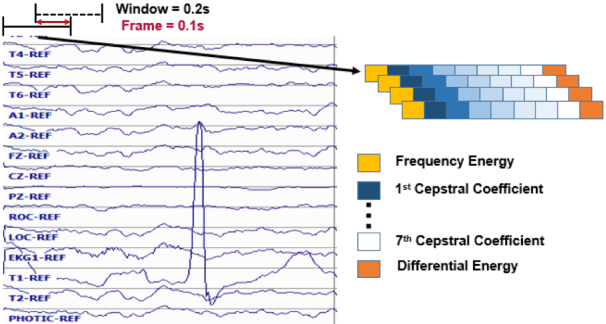
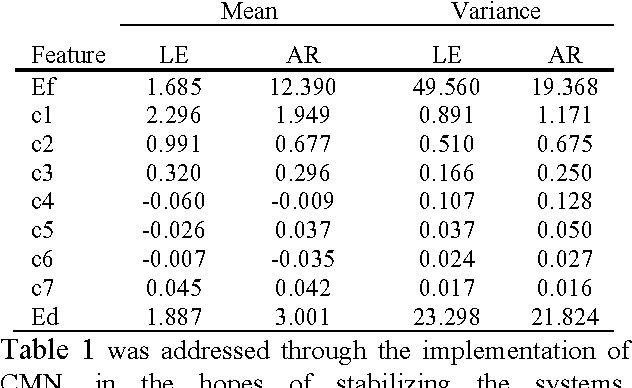
Clinical electroencephalographic (EEG) data varies significantly depending on a number of operational conditions (e.g., the type and placement of electrodes, the type of electrical grounding used). This investigation explores the statistical differences present in two different referential montages: Linked Ear (LE) and Averaged Reference (AR). Each of these accounts for approximately 45% of the data in the TUH EEG Corpus. In this study, we explore the impact this variability has on machine learning performance. We compare the statistical properties of features generated using these two montages, and explore the impact of performance on our standard Hidden Markov Model (HMM) based classification system. We show that a system trained on LE data significantly outperforms one trained only on AR data (77.2% vs. 61.4%). We also demonstrate that performance of a system trained on both data sets is somewhat compromised (71.4% vs. 77.2%). A statistical analysis of the data suggests that mean, variance and channel normalization should be considered. However, cepstral mean subtraction failed to produce an improvement in performance, suggesting that the impact of these statistical differences is subtler.

Online Learning with Automata-based Expert Sequences

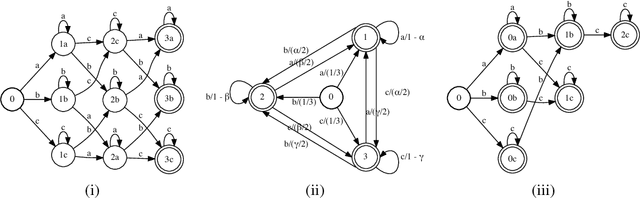
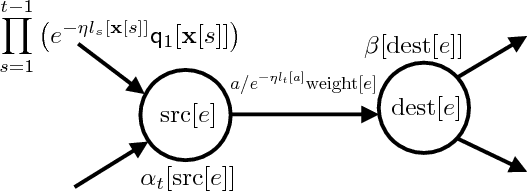
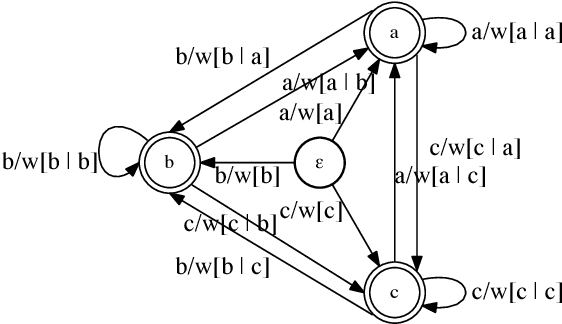
We consider a general framework of online learning with expert advice where regret is defined with respect to sequences of experts accepted by a weighted automaton. Our framework covers several problems previously studied, including competing against k-shifting experts. We give a series of algorithms for this problem, including an automata-based algorithm extending weighted-majority and more efficient algorithms based on the notion of failure transitions. We further present efficient algorithms based on an approximation of the competitor automaton, in particular n-gram models obtained by minimizing the \infty-R\'{e}nyi divergence, and present an extensive study of the approximation properties of such models. Finally, we also extend our algorithms and results to the framework of sleeping experts.

AdaNet: Adaptive Structural Learning of Artificial Neural Networks

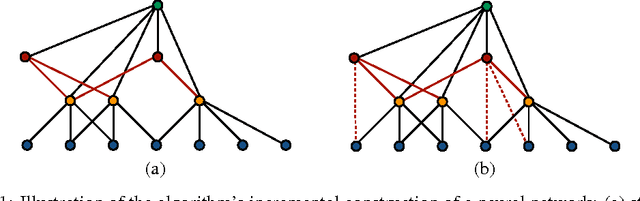
We present new algorithms for adaptively learning artificial neural networks. Our algorithms (AdaNet) adaptively learn both the structure of the network and its weights. They are based on a solid theoretical analysis, including data-dependent generalization guarantees that we prove and discuss in detail. We report the results of large-scale experiments with one of our algorithms on several binary classification tasks extracted from the CIFAR-10 dataset. The results demonstrate that our algorithm can automatically learn network structures with very competitive performance accuracies when compared with those achieved for neural networks found by standard approaches.

Structured Prediction Theory Based on Factor Graph Complexity

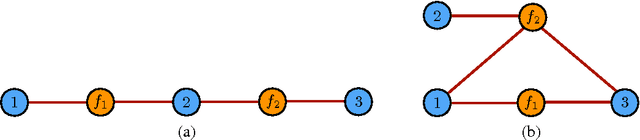
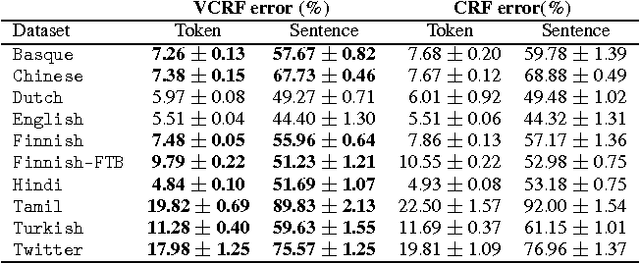
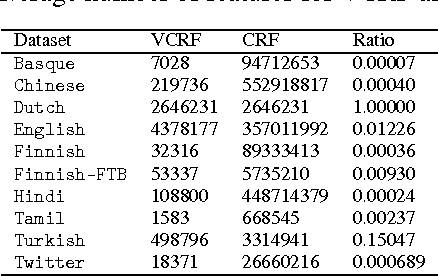
We present a general theoretical analysis of structured prediction with a series of new results. We give new data-dependent margin guarantees for structured prediction for a very wide family of loss functions and a general family of hypotheses, with an arbitrary factor graph decomposition. These are the tightest margin bounds known for both standard multi-class and general structured prediction problems. Our guarantees are expressed in terms of a data-dependent complexity measure, factor graph complexity, which we show can be estimated from data and bounded in terms of familiar quantities. We further extend our theory by leveraging the principle of Voted Risk Minimization (VRM) and show that learning is possible even with complex factor graphs. We present new learning bounds for this advanced setting, which we use to design two new algorithms, Voted Conditional Random Field (VCRF) and Voted Structured Boosting (StructBoost). These algorithms can make use of complex features and factor graphs and yet benefit from favorable learning guarantees. We also report the results of experiments with VCRF on several datasets to validate our theory.

Accelerating Optimization via Adaptive Prediction

We present a powerful general framework for designing data-dependent optimization algorithms, building upon and unifying recent techniques in adaptive regularization, optimistic gradient predictions, and problem-dependent randomization. We first present a series of new regret guarantees that hold at any time and under very minimal assumptions, and then show how different relaxations recover existing algorithms, both basic as well as more recent sophisticated ones. Finally, we show how combining adaptivity, optimism, and problem-dependent randomization can guide the design of algorithms that benefit from more favorable guarantees than recent state-of-the-art methods.