Structured Prediction Theory Based on Factor Graph Complexity
Paper and Code
Dec 01, 2016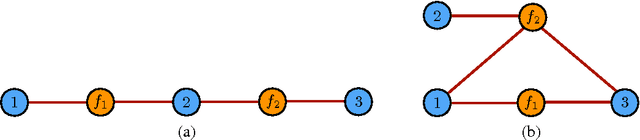
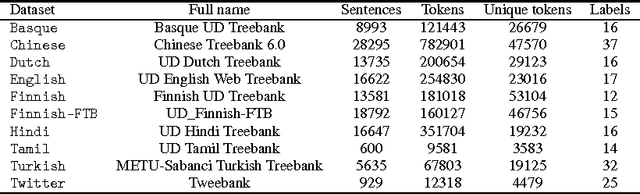
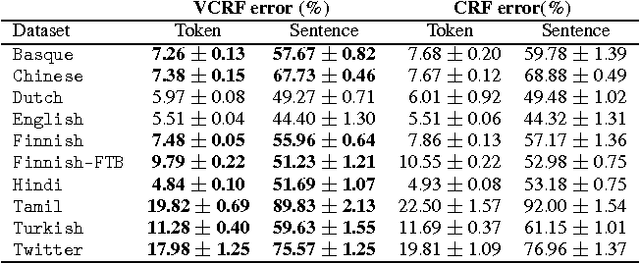
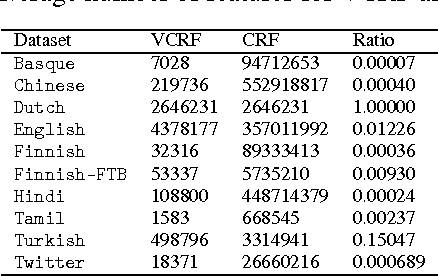
We present a general theoretical analysis of structured prediction with a series of new results. We give new data-dependent margin guarantees for structured prediction for a very wide family of loss functions and a general family of hypotheses, with an arbitrary factor graph decomposition. These are the tightest margin bounds known for both standard multi-class and general structured prediction problems. Our guarantees are expressed in terms of a data-dependent complexity measure, factor graph complexity, which we show can be estimated from data and bounded in terms of familiar quantities. We further extend our theory by leveraging the principle of Voted Risk Minimization (VRM) and show that learning is possible even with complex factor graphs. We present new learning bounds for this advanced setting, which we use to design two new algorithms, Voted Conditional Random Field (VCRF) and Voted Structured Boosting (StructBoost). These algorithms can make use of complex features and factor graphs and yet benefit from favorable learning guarantees. We also report the results of experiments with VCRF on several datasets to validate our theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge