DART: A Principled Approach to Adversarially Robust Unsupervised Domain Adaptation

Distribution shifts and adversarial examples are two major challenges for deploying machine learning models. While these challenges have been studied individually, their combination is an important topic that remains relatively under-explored. In this work, we study the problem of adversarial robustness under a common setting of distribution shift - unsupervised domain adaptation (UDA). Specifically, given a labeled source domain $D_S$ and an unlabeled target domain $D_T$ with related but different distributions, the goal is to obtain an adversarially robust model for $D_T$. The absence of target domain labels poses a unique challenge, as conventional adversarial robustness defenses cannot be directly applied to $D_T$. To address this challenge, we first establish a generalization bound for the adversarial target loss, which consists of (i) terms related to the loss on the data, and (ii) a measure of worst-case domain divergence. Motivated by this bound, we develop a novel unified defense framework called Divergence Aware adveRsarial Training (DART), which can be used in conjunction with a variety of standard UDA methods; e.g., DANN [Ganin and Lempitsky, 2015]. DART is applicable to general threat models, including the popular $\ell_p$-norm model, and does not require heuristic regularizers or architectural changes. We also release DomainRobust: a testbed for evaluating robustness of UDA models to adversarial attacks. DomainRobust consists of 4 multi-domain benchmark datasets (with 46 source-target pairs) and 7 meta-algorithms with a total of 11 variants. Our large-scale experiments demonstrate that on average, DART significantly enhances model robustness on all benchmarks compared to the state of the art, while maintaining competitive standard accuracy. The relative improvement in robustness from DART reaches up to 29.2% on the source-target domain pairs considered.

Leveraging Importance Weights in Subset Selection

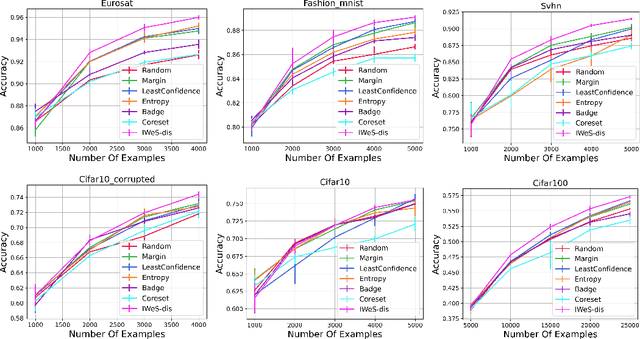
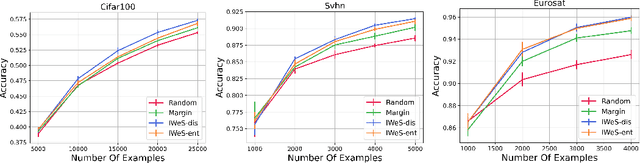
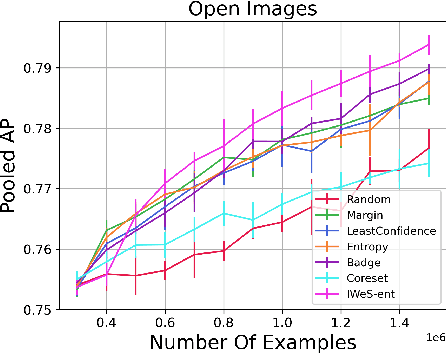
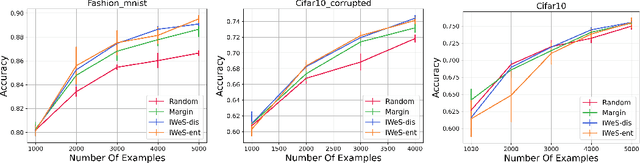
We present a subset selection algorithm designed to work with arbitrary model families in a practical batch setting. In such a setting, an algorithm can sample examples one at a time but, in order to limit overhead costs, is only able to update its state (i.e. further train model weights) once a large enough batch of examples is selected. Our algorithm, IWeS, selects examples by importance sampling where the sampling probability assigned to each example is based on the entropy of models trained on previously selected batches. IWeS admits significant performance improvement compared to other subset selection algorithms for seven publicly available datasets. Additionally, it is competitive in an active learning setting, where the label information is not available at selection time. We also provide an initial theoretical analysis to support our importance weighting approach, proving generalization and sampling rate bounds.

OWA aggregation of multi-criteria with mixed uncertain fuzzy satisfactions

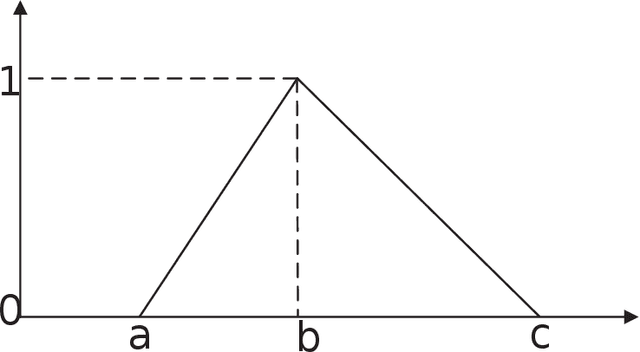
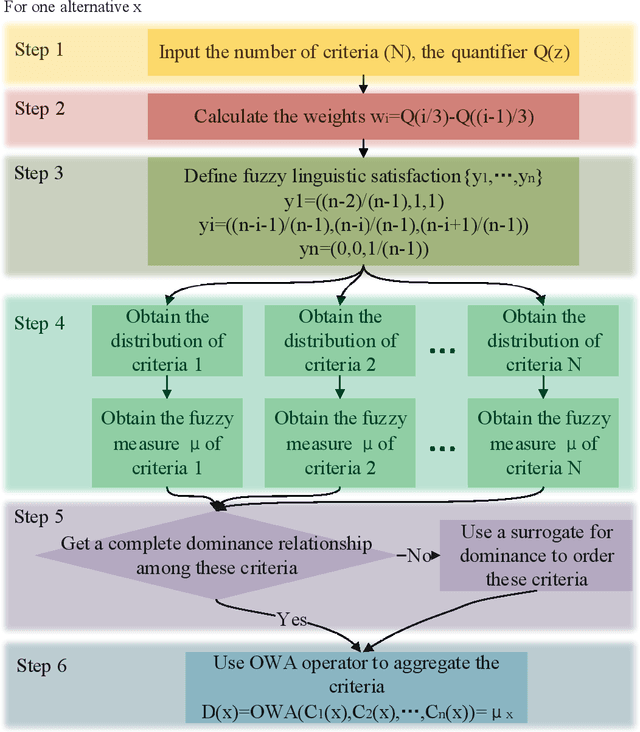
We apply the Ordered Weighted Averaging (OWA) operator in multi-criteria decision-making. To satisfy different kinds of uncertainty, measure based dominance has been presented to gain the order of different criterion. However, this idea has not been applied in fuzzy system until now. In this paper, we focus on the situation where the linguistic satisfactions are fuzzy measures instead of the exact values. We review the concept of OWA operator and discuss the order mechanism of fuzzy number. Then we combine with measure-based dominance to give an overall score of each alternatives. An example is illustrated to show the whole procedure.

Thompson Sampling for a Fatigue-aware Online Recommendation System

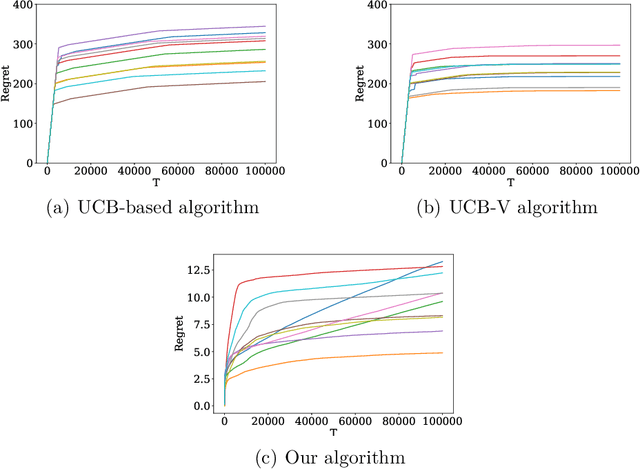
In this paper we consider an online recommendation setting, where a platform recommends a sequence of items to its users at every time period. The users respond by selecting one of the items recommended or abandon the platform due to fatigue from seeing less useful items. Assuming a parametric stochastic model of user behavior, which captures positional effects of these items as well as the abandoning behavior of users, the platform's goal is to recommend sequences of items that are competitive to the single best sequence of items in hindsight, without knowing the true user model a priori. Naively applying a stochastic bandit algorithm in this setting leads to an exponential dependence on the number of items. We propose a new Thompson sampling based algorithm with expected regret that is polynomial in the number of items in this combinatorial setting, and performs extremely well in practice. We also show a contextual version of our solution.