Benjamin Coleman
Dima
AgenticTagger: Structured Item Representation for Recommendation with LLM Agents
Feb 05, 2026Abstract:High-quality representations are a core requirement for effective recommendation. In this work, we study the problem of LLM-based descriptor generation, i.e., keyphrase-like natural language item representation generation frameworks with minimal constraints on downstream applications. We propose AgenticTagger, a framework that queries LLMs for representing items with sequences of text descriptors. However, open-ended generation provides little control over the generation space, leading to high cardinality, low-performance descriptors that renders downstream modeling challenging. To this end, AgenticTagger features two core stages: (1) a vocabulary building stage where a set of hierarchical, low-cardinality, and high-quality descriptors is identified, and (2) a vocabulary assignment stage where LLMs assign in-vocabulary descriptors to items. To effectively and efficiently ground vocabulary in the item corpus of interest, we design a multi-agent reflection mechanism where an architect LLM iteratively refines the vocabulary guided by parallelized feedback from annotator LLMs that validates the vocabulary against item data. Experiments on public and private data show AgenticTagger brings consistent improvements across diverse recommendation scenarios, including generative and term-based retrieval, ranking, and controllability-oriented, critique-based recommendation.
PACEvolve: Enabling Long-Horizon Progress-Aware Consistent Evolution
Jan 15, 2026Abstract:Large Language Models (LLMs) have emerged as powerful operators for evolutionary search, yet the design of efficient search scaffolds remains ad hoc. While promising, current LLM-in-the-loop systems lack a systematic approach to managing the evolutionary process. We identify three distinct failure modes: Context Pollution, where experiment history biases future candidate generation; Mode Collapse, where agents stagnate in local minima due to poor exploration-exploitation balance; and Weak Collaboration, where rigid crossover strategies fail to leverage parallel search trajectories effectively. We introduce Progress-Aware Consistent Evolution (PACEvolve), a framework designed to robustly govern the agent's context and search dynamics, to address these challenges. PACEvolve combines hierarchical context management (HCM) with pruning to address context pollution; momentum-based backtracking (MBB) to escape local minima; and a self-adaptive sampling policy that unifies backtracking and crossover for dynamic search coordination (CE), allowing agents to balance internal refinement with cross-trajectory collaboration. We demonstrate that PACEvolve provides a systematic path to consistent, long-horizon self-improvement, achieving state-of-the-art results on LLM-SR and KernelBench, while discovering solutions surpassing the record on Modded NanoGPT.
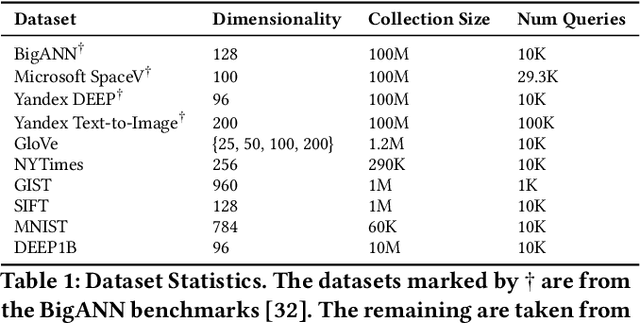
Breaking the Curse of Dimensionality: On the Stability of Modern Vector Retrieval
Dec 13, 2025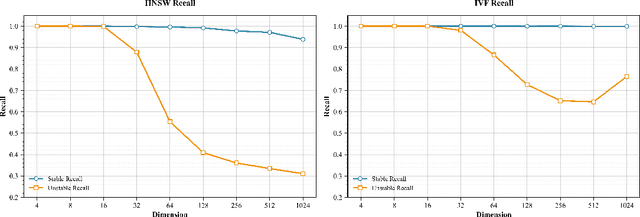
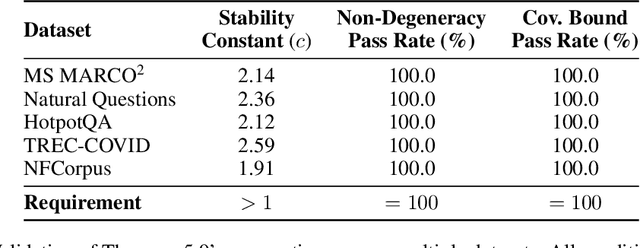
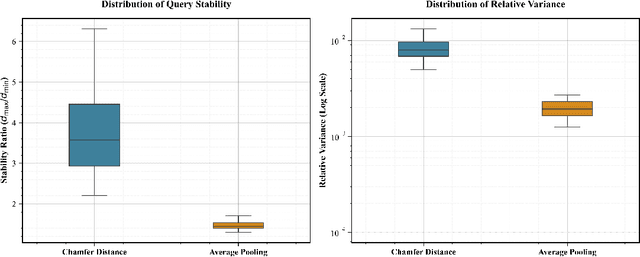
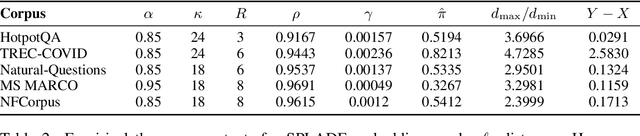
Abstract:Modern vector databases enable efficient retrieval over high-dimensional neural embeddings, powering applications from web search to retrieval-augmented generation. However, classical theory predicts such tasks should suffer from the curse of dimensionality, where distances between points become nearly indistinguishable, thereby crippling efficient nearest-neighbor search. We revisit this paradox through the lens of stability, the property that small perturbations to a query do not radically alter its nearest neighbors. Building on foundational results, we extend stability theory to three key retrieval settings widely used in practice: (i) multi-vector search, where we prove that the popular Chamfer distance metric preserves single-vector stability, while average pooling aggregation may destroy it; (ii) filtered vector search, where we show that sufficiently large penalties for mismatched filters can induce stability even when the underlying search is unstable; and (iii) sparse vector search, where we formalize and prove novel sufficient stability conditions. Across synthetic and real datasets, our experimental results match our theoretical predictions, offering concrete guidance for model and system design to avoid the curse of dimensionality.
Gemma 3 Technical Report
Mar 25, 2025Abstract:We introduce Gemma 3, a multimodal addition to the Gemma family of lightweight open models, ranging in scale from 1 to 27 billion parameters. This version introduces vision understanding abilities, a wider coverage of languages and longer context - at least 128K tokens. We also change the architecture of the model to reduce the KV-cache memory that tends to explode with long context. This is achieved by increasing the ratio of local to global attention layers, and keeping the span on local attention short. The Gemma 3 models are trained with distillation and achieve superior performance to Gemma 2 for both pre-trained and instruction finetuned versions. In particular, our novel post-training recipe significantly improves the math, chat, instruction-following and multilingual abilities, making Gemma3-4B-IT competitive with Gemma2-27B-IT and Gemma3-27B-IT comparable to Gemini-1.5-Pro across benchmarks. We release all our models to the community.
Down with the Hierarchy: The 'H' in HNSW Stands for "Hubs"
Dec 02, 2024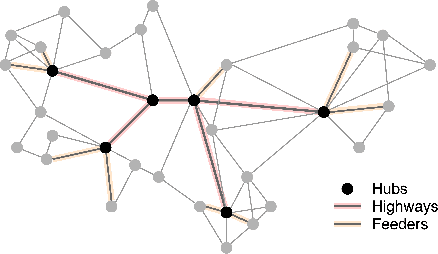
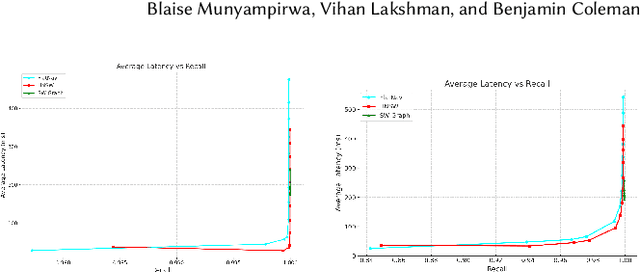

Abstract:Driven by recent breakthrough advances in neural representation learning, approximate near-neighbor (ANN) search over vector embeddings has emerged as a critical computational workload. With the introduction of the seminal Hierarchical Navigable Small World (HNSW) algorithm, graph-based indexes have established themseves as the overwhelmingly dominant paradigm for efficient and scalable ANN search. As the name suggests, HNSW searches a layered hierarchical graph to quickly identify neighborhoods of similar points to a given query vector. But is this hierarchy even necessary? A rigorous experimental analysis to answer this question would provide valuable insights into the nature of algorithm design for ANN search and motivate directions for future work in this increasingly crucial domain. To that end, we conduct an extensive benchmarking study covering more large-scale datasets than prior investigations of this question. We ultimately find that a flat graph retains all of the benefits of HNSW on high-dimensional datasets, with latency and recall performance essentially \emph{identical} to the original algorithm but with less memory overhead. Furthermore, we go a step further and study \emph{why} the hierarchy of HNSW provides no benefit in high dimensions, hypothesizing that navigable small world graphs contain a well-connected, frequently traversed ``highway" of hub nodes that maintain the same purported function as the hierarchical layers. We present compelling empirical evidence that the \emph{Hub Highway Hypothesis} holds for real datasets and investigate the mechanisms by which the highway forms. The implications of this hypothesis may also provide future research directions in developing enhancements to graph-based ANN search.
How to Train Data-Efficient LLMs
Feb 15, 2024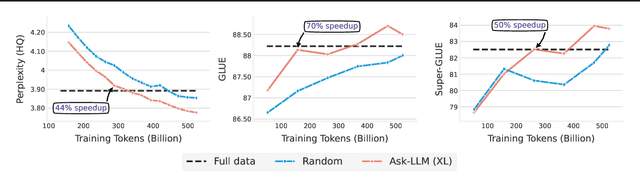
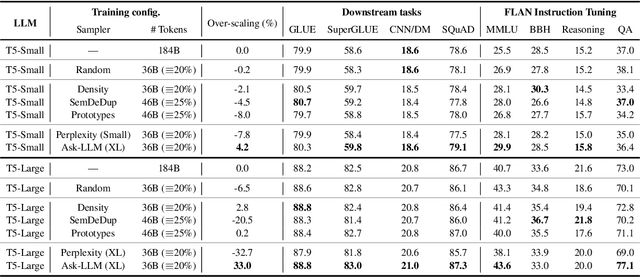
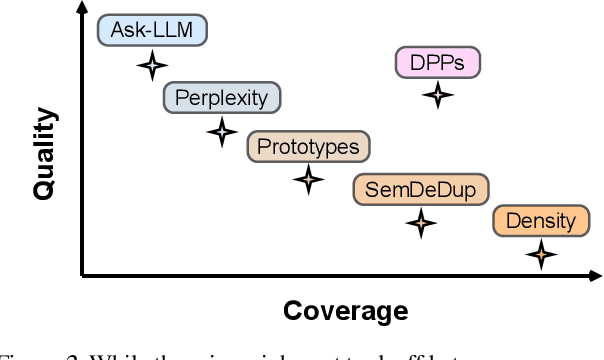

Abstract:The training of large language models (LLMs) is expensive. In this paper, we study data-efficient approaches for pre-training LLMs, i.e., techniques that aim to optimize the Pareto frontier of model quality and training resource/data consumption. We seek to understand the tradeoffs associated with data selection routines based on (i) expensive-to-compute data-quality estimates, and (ii) maximization of coverage and diversity-based measures in the feature space. Our first technique, Ask-LLM, leverages the zero-shot reasoning capabilities of instruction-tuned LLMs to directly assess the quality of a training example. To target coverage, we propose Density sampling, which models the data distribution to select a diverse sample. In our comparison of 19 samplers, involving hundreds of evaluation tasks and pre-training runs, we find that Ask-LLM and Density are the best methods in their respective categories. Coverage sampling can recover the performance of the full data, while models trained on Ask-LLM data consistently outperform full-data training -- even when we reject 90% of the original dataset, while converging up to 70% faster.
Adaptive Sampling for Deep Learning via Efficient Nonparametric Proxies
Nov 22, 2023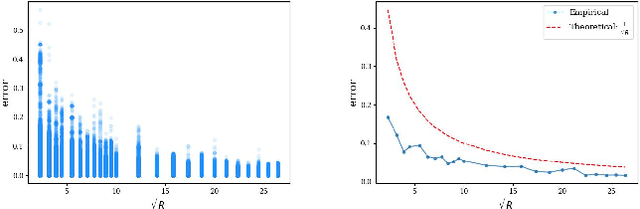
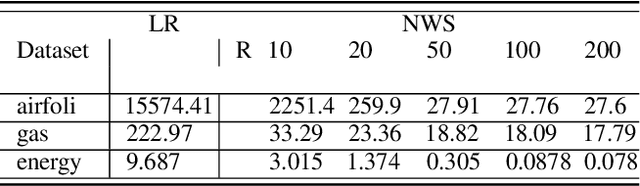
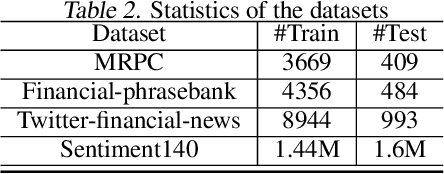
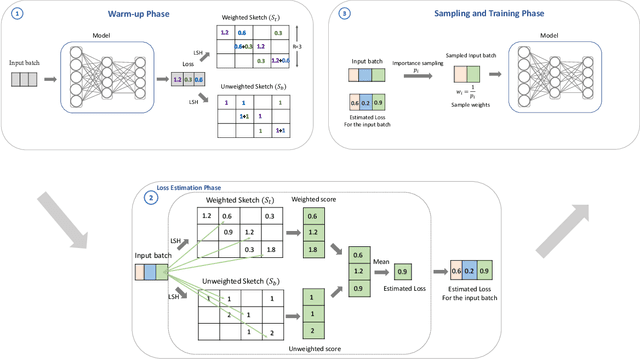
Abstract:Data sampling is an effective method to improve the training speed of neural networks, with recent results demonstrating that it can even break the neural scaling laws. These results critically rely on high-quality scores to estimate the importance of an input to the network. We observe that there are two dominant strategies: static sampling, where the scores are determined before training, and dynamic sampling, where the scores can depend on the model weights. Static algorithms are computationally inexpensive but less effective than their dynamic counterparts, which can cause end-to-end slowdown due to their need to explicitly compute losses. To address this problem, we propose a novel sampling distribution based on nonparametric kernel regression that learns an effective importance score as the neural network trains. However, nonparametric regression models are too computationally expensive to accelerate end-to-end training. Therefore, we develop an efficient sketch-based approximation to the Nadaraya-Watson estimator. Using recent techniques from high-dimensional statistics and randomized algorithms, we prove that our Nadaraya-Watson sketch approximates the estimator with exponential convergence guarantees. Our sampling algorithm outperforms the baseline in terms of wall-clock time and accuracy on four datasets.
CAPS: A Practical Partition Index for Filtered Similarity Search
Aug 29, 2023



Abstract:With the surging popularity of approximate near-neighbor search (ANNS), driven by advances in neural representation learning, the ability to serve queries accompanied by a set of constraints has become an area of intense interest. While the community has recently proposed several algorithms for constrained ANNS, almost all of these methods focus on integration with graph-based indexes, the predominant class of algorithms achieving state-of-the-art performance in latency-recall tradeoffs. In this work, we take a different approach and focus on developing a constrained ANNS algorithm via space partitioning as opposed to graphs. To that end, we introduce Constrained Approximate Partitioned Search (CAPS), an index for ANNS with filters via space partitions that not only retains the benefits of a partition-based algorithm but also outperforms state-of-the-art graph-based constrained search techniques in recall-latency tradeoffs, with only 10% of the index size.
CARAMEL: A Succinct Read-Only Lookup Table via Compressed Static Functions
May 26, 2023


Abstract:Lookup tables are a fundamental structure in many data processing and systems applications. Examples include tokenized text in NLP, quantized embedding collections in recommendation systems, integer sketches for streaming data, and hash-based string representations in genomics. With the increasing size of web-scale data, such applications often require compression techniques that support fast random $O(1)$ lookup of individual parameters directly on the compressed data (i.e. without blockwise decompression in RAM). While the community has proposd a number of succinct data structures that support queries over compressed representations, these approaches do not fully leverage the low-entropy structure prevalent in real-world workloads to reduce space. Inspired by recent advances in static function construction techniques, we propose a space-efficient representation of immutable key-value data, called CARAMEL, specifically designed for the case where the values are multi-sets. By carefully combining multiple compressed static functions, CARAMEL occupies space proportional to the data entropy with low memory overheads and minimal lookup costs. We demonstrate 1.25-16x compression on practical lookup tasks drawn from real-world systems, improving upon established techniques, including a production-grade read-only database widely used for development within Amazon.com.
Unified Embedding: Battle-Tested Feature Representations for Web-Scale ML Systems
May 20, 2023Abstract:Learning high-quality feature embeddings efficiently and effectively is critical for the performance of web-scale machine learning systems. A typical model ingests hundreds of features with vocabularies on the order of millions to billions of tokens. The standard approach is to represent each feature value as a d-dimensional embedding, introducing hundreds of billions of parameters for extremely high-cardinality features. This bottleneck has led to substantial progress in alternative embedding algorithms. Many of these methods, however, make the assumption that each feature uses an independent embedding table. This work introduces a simple yet highly effective framework, Feature Multiplexing, where one single representation space is used across many different categorical features. Our theoretical and empirical analysis reveals that multiplexed embeddings can be decomposed into components from each constituent feature, allowing models to distinguish between features. We show that multiplexed representations lead to Pareto-optimal parameter-accuracy tradeoffs for three public benchmark datasets. Further, we propose a highly practical approach called Unified Embedding with three major benefits: simplified feature configuration, strong adaptation to dynamic data distributions, and compatibility with modern hardware. Unified embedding gives significant improvements in offline and online metrics compared to highly competitive baselines across five web-scale search, ads, and recommender systems, where it serves billions of users across the world in industry-leading products.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge