Pipeline Parallelism for DNN Inference with Practical Performance Guarantees

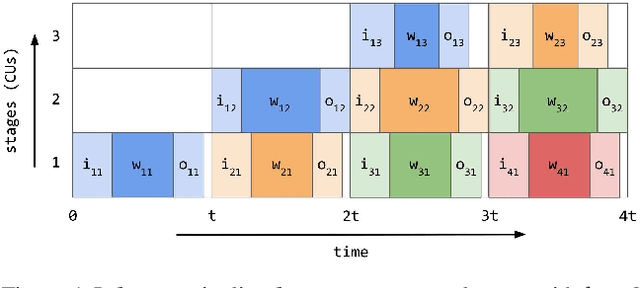
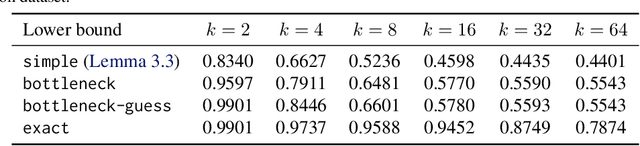
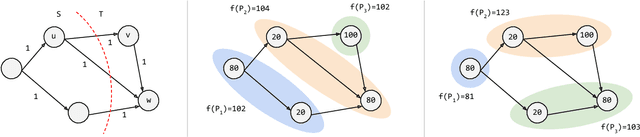
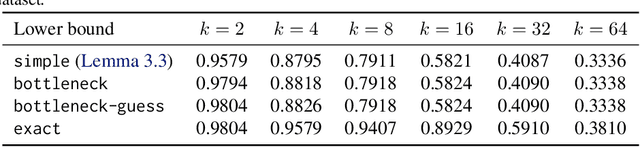
We optimize pipeline parallelism for deep neural network (DNN) inference by partitioning model graphs into $k$ stages and minimizing the running time of the bottleneck stage, including communication. We design practical algorithms for this NP-hard problem and show that they are nearly optimal in practice by comparing against strong lower bounds obtained via novel mixed-integer programming (MIP) formulations. We apply these algorithms and lower-bound methods to production models to achieve substantially improved approximation guarantees compared to standard combinatorial lower bounds. For example, evaluated via geometric means across production data with $k=16$ pipeline stages, our MIP formulations more than double the lower bounds, improving the approximation ratio from $2.175$ to $1.058$. This work shows that while max-throughput partitioning is theoretically hard, we have a handle on the algorithmic side of the problem in practice and much of the remaining challenge is in developing more accurate cost models to feed into the partitioning algorithms.

A Transferable Approach for Partitioning Machine Learning Models on Multi-Chip-Modules

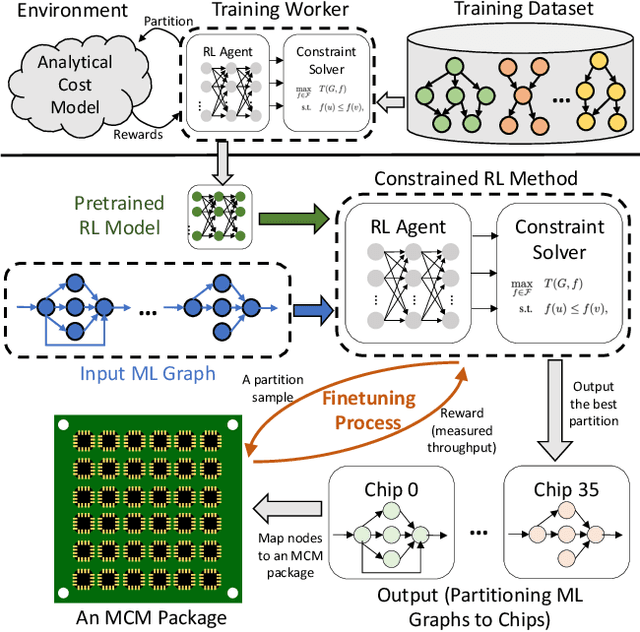
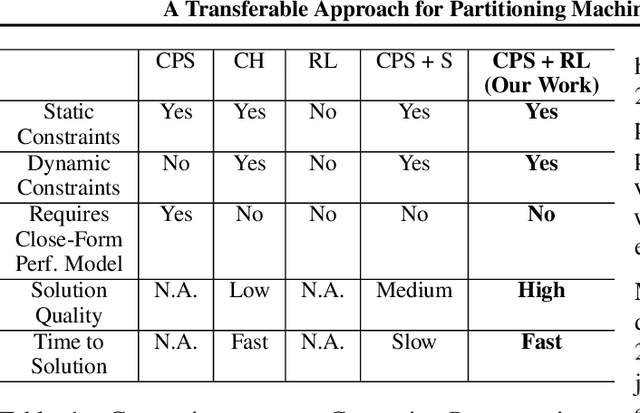
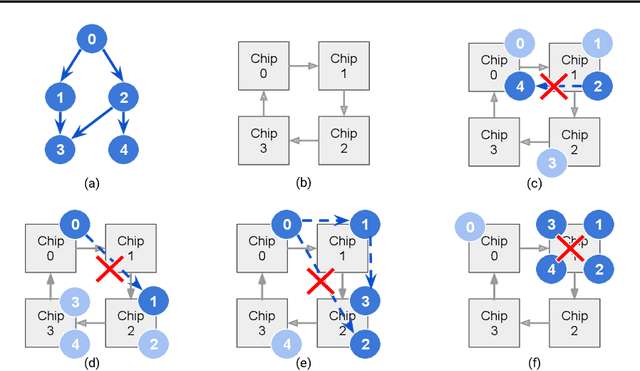
Multi-Chip-Modules (MCMs) reduce the design and fabrication cost of machine learning (ML) accelerators while delivering performance and energy efficiency on par with a monolithic large chip. However, ML compilers targeting MCMs need to solve complex optimization problems optimally and efficiently to achieve this high performance. One such problem is the multi-chip partitioning problem where compilers determine the optimal partitioning and placement of operations in tensor computation graphs on chiplets in MCMs. Partitioning ML graphs for MCMs is particularly hard as the search space grows exponentially with the number of chiplets available and the number of nodes in the neural network. Furthermore, the constraints imposed by the underlying hardware produce a search space where valid solutions are extremely sparse. In this paper, we present a strategy using a deep reinforcement learning (RL) framework to emit a possibly invalid candidate partition that is then corrected by a constraint solver. Using the constraint solver ensures that RL encounters valid solutions in the sparse space frequently enough to converge with fewer samples as compared to non-learned strategies. The architectural choices we make for the policy network allow us to generalize across different ML graphs. Our evaluation of a production-scale model, BERT, on real hardware reveals that the partitioning generated using RL policy achieves 6.11% and 5.85% higher throughput than random search and simulated annealing. In addition, fine-tuning the pre-trained RL policy reduces the search time from 3 hours to only 9 minutes, while achieving the same throughput as training RL policy from scratch.