Aaron Archer
Pipeline Parallelism for DNN Inference with Practical Performance Guarantees
Nov 07, 2023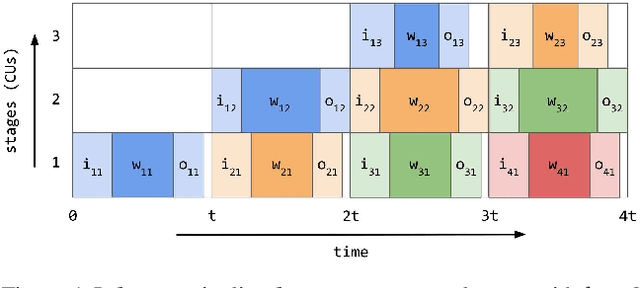
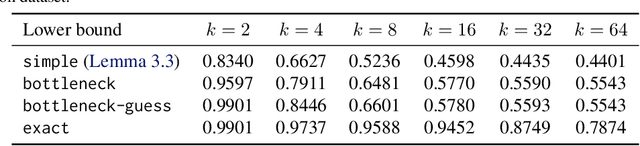
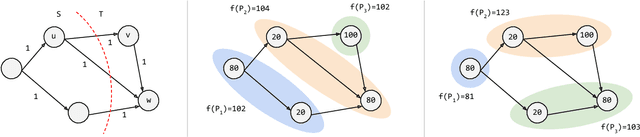
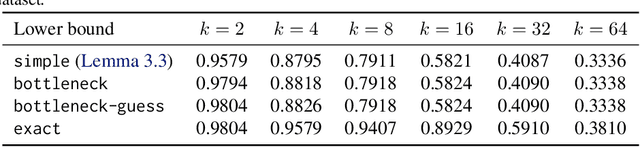
Abstract:We optimize pipeline parallelism for deep neural network (DNN) inference by partitioning model graphs into $k$ stages and minimizing the running time of the bottleneck stage, including communication. We design practical algorithms for this NP-hard problem and show that they are nearly optimal in practice by comparing against strong lower bounds obtained via novel mixed-integer programming (MIP) formulations. We apply these algorithms and lower-bound methods to production models to achieve substantially improved approximation guarantees compared to standard combinatorial lower bounds. For example, evaluated via geometric means across production data with $k=16$ pipeline stages, our MIP formulations more than double the lower bounds, improving the approximation ratio from $2.175$ to $1.058$. This work shows that while max-throughput partitioning is theoretically hard, we have a handle on the algorithmic side of the problem in practice and much of the remaining challenge is in developing more accurate cost models to feed into the partitioning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge