Distribution Preference Optimization: A Fine-grained Perspective for LLM Unlearning

As Large Language Models (LLMs) demonstrate remarkable capabilities learned from vast corpora, concerns regarding data privacy and safety are receiving increasing attention. LLM unlearning, which aims to remove the influence of specific data while preserving overall model utility, is becoming an important research area. One of the mainstream unlearning classes is optimization-based methods, which achieve forgetting directly through fine-tuning, exemplified by Negative Preference Optimization (NPO). However, NPO's effectiveness is limited by its inherent lack of explicit positive preference signals. Attempts to introduce such signals by constructing preferred responses often necessitate domain-specific knowledge or well-designed prompts, fundamentally restricting their generalizability. In this paper, we shift the focus to the distribution-level, directly targeting the next-token probability distribution instead of entire responses, and derive a novel unlearning algorithm termed \textbf{Di}stribution \textbf{P}reference \textbf{O}ptimization (DiPO). We show that the requisite preference distribution pairs for DiPO, which are distributions over the model's output tokens, can be constructed by selectively amplifying or suppressing the model's high-confidence output logits, thereby effectively overcoming NPO's limitations. We theoretically prove the consistency of DiPO's loss function with the desired unlearning direction. Extensive experiments demonstrate that DiPO achieves a strong trade-off between model utility and forget quality. Notably, DiPO attains the highest forget quality on the TOFU benchmark, and maintains leading scalability and sustainability in utility preservation on the MUSE benchmark.

Reinforcement Fine-Tuning Powers Reasoning Capability of Multimodal Large Language Models

Standing in 2025, at a critical juncture in the pursuit of Artificial General Intelligence (AGI), reinforcement fine-tuning (RFT) has demonstrated significant potential in enhancing the reasoning capability of large language models (LLMs) and has led to the development of cutting-edge AI models such as OpenAI-o1 and DeepSeek-R1. Moreover, the efficient application of RFT to enhance the reasoning capability of multimodal large language models (MLLMs) has attracted widespread attention from the community. In this position paper, we argue that reinforcement fine-tuning powers the reasoning capability of multimodal large language models. To begin with, we provide a detailed introduction to the fundamental background knowledge that researchers interested in this field should be familiar with. Furthermore, we meticulously summarize the improvements of RFT in powering reasoning capability of MLLMs into five key points: diverse modalities, diverse tasks and domains, better training algorithms, abundant benchmarks and thriving engineering frameworks. Finally, we propose five promising directions for future research that the community might consider. We hope that this position paper will provide valuable insights to the community at this pivotal stage in the advancement toward AGI. Summary of works done on RFT for MLLMs is available at https://github.com/Sun-Haoyuan23/Awesome-RL-based-Reasoning-MLLMs.

In-Context Learning of Polynomial Kernel Regression in Transformers with GLU Layers

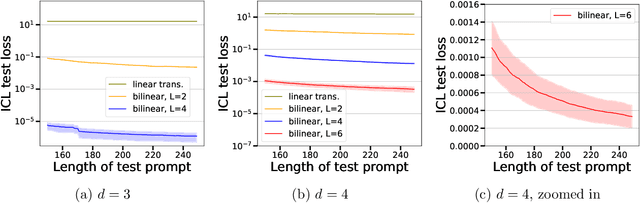
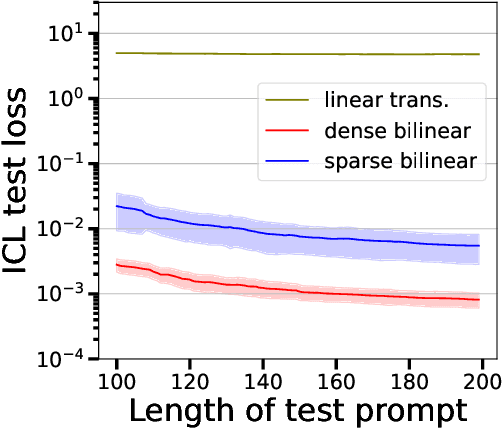
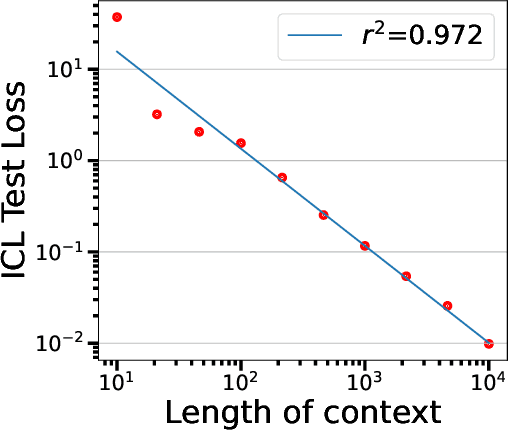
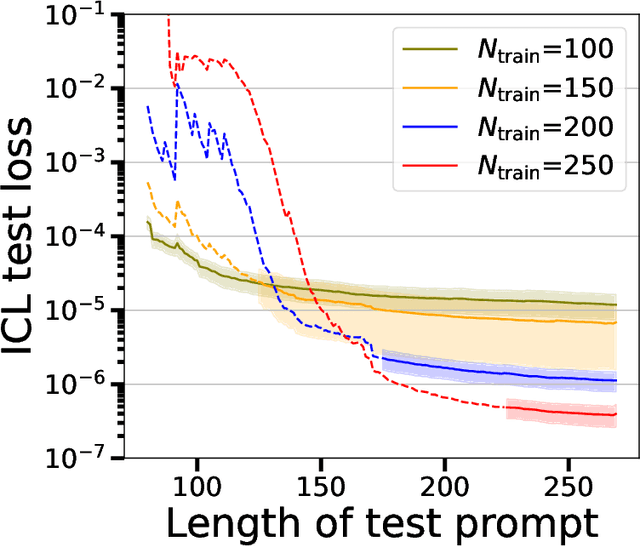
Transformer-based models have demonstrated remarkable ability in in-context learning (ICL), where they can adapt to unseen tasks from a prompt with a few examples, without requiring parameter updates. Recent research has provided insight into how linear Transformers can perform ICL by implementing gradient descent estimators. In particular, it has been shown that the optimal linear self-attention (LSA) mechanism can implement one step of gradient descent with respect to a linear least-squares objective when trained on random linear regression tasks. However, the theoretical understanding of ICL for nonlinear function classes remains limited. In this work, we address this gap by first showing that LSA is inherently restricted to solving linear least-squares objectives and thus, the solutions in prior works cannot readily extend to nonlinear ICL tasks. To overcome this limitation, drawing inspiration from modern architectures, we study a mechanism that combines LSA with GLU-like feed-forward layers and show that this allows the model to perform one step of gradient descent on a polynomial kernel regression. Further, we characterize the scaling behavior of the resulting Transformer model, highlighting the necessary model size to effectively handle quadratic ICL tasks. Our findings highlight the distinct roles of attention and feed-forward layers in nonlinear ICL and identify key challenges when extending ICL to nonlinear function classes.

Generalizing Alignment Paradigm of Text-to-Image Generation with Preferences through $f$-divergence Minimization

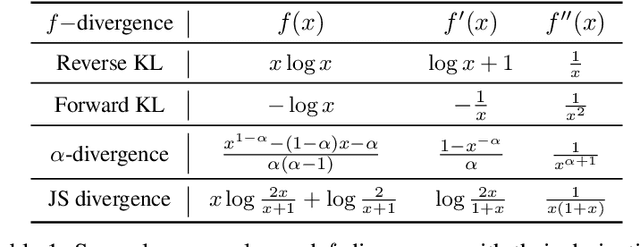
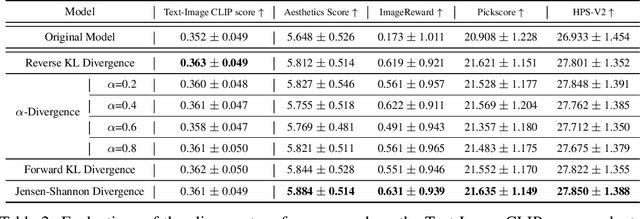
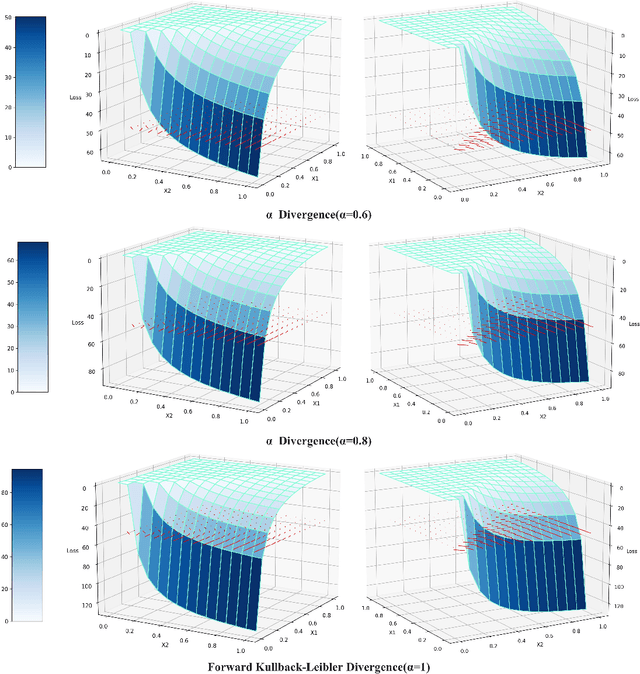
Direct Preference Optimization (DPO) has recently expanded its successful application from aligning large language models (LLMs) to aligning text-to-image models with human preferences, which has generated considerable interest within the community. However, we have observed that these approaches rely solely on minimizing the reverse Kullback-Leibler divergence during alignment process between the fine-tuned model and the reference model, neglecting the incorporation of other divergence constraints. In this study, we focus on extending reverse Kullback-Leibler divergence in the alignment paradigm of text-to-image models to $f$-divergence, which aims to garner better alignment performance as well as good generation diversity. We provide the generalized formula of the alignment paradigm under the $f$-divergence condition and thoroughly analyze the impact of different divergence constraints on alignment process from the perspective of gradient fields. We conduct comprehensive evaluation on image-text alignment performance, human value alignment performance and generation diversity performance under different divergence constraints, and the results indicate that alignment based on Jensen-Shannon divergence achieves the best trade-off among them. The option of divergence employed for aligning text-to-image models significantly impacts the trade-off between alignment performance (especially human value alignment) and generation diversity, which highlights the necessity of selecting an appropriate divergence for practical applications.

A Method on Searching Better Activation Functions

The success of artificial neural networks (ANNs) hinges greatly on the judicious selection of an activation function, introducing non-linearity into network and enabling them to model sophisticated relationships in data. However, the search of activation functions has largely relied on empirical knowledge in the past, lacking theoretical guidance, which has hindered the identification of more effective activation functions. In this work, we offer a proper solution to such issue. Firstly, we theoretically demonstrate the existence of the worst activation function with boundary conditions (WAFBC) from the perspective of information entropy. Furthermore, inspired by the Taylor expansion form of information entropy functional, we propose the Entropy-based Activation Function Optimization (EAFO) methodology. EAFO methodology presents a novel perspective for designing static activation functions in deep neural networks and the potential of dynamically optimizing activation during iterative training. Utilizing EAFO methodology, we derive a novel activation function from ReLU, known as Correction Regularized ReLU (CRReLU). Experiments conducted with vision transformer and its variants on CIFAR-10, CIFAR-100 and ImageNet-1K datasets demonstrate the superiority of CRReLU over existing corrections of ReLU. Extensive empirical studies on task of large language model (LLM) fine-tuning, CRReLU exhibits superior performance compared to GELU, suggesting its broader potential for practical applications.

Improving Offline Reinforcement Learning with Inaccurate Simulators

Offline reinforcement learning (RL) provides a promising approach to avoid costly online interaction with the real environment. However, the performance of offline RL highly depends on the quality of the datasets, which may cause extrapolation error in the learning process. In many robotic applications, an inaccurate simulator is often available. However, the data directly collected from the inaccurate simulator cannot be directly used in offline RL due to the well-known exploration-exploitation dilemma and the dynamic gap between inaccurate simulation and the real environment. To address these issues, we propose a novel approach to combine the offline dataset and the inaccurate simulation data in a better manner. Specifically, we pre-train a generative adversarial network (GAN) model to fit the state distribution of the offline dataset. Given this, we collect data from the inaccurate simulator starting from the distribution provided by the generator and reweight the simulated data using the discriminator. Our experimental results in the D4RL benchmark and a real-world manipulation task confirm that our method can benefit more from both inaccurate simulator and limited offline datasets to achieve better performance than the state-of-the-art methods.

A least-square method for non-asymptotic identification in linear switching control

The focus of this paper is on linear system identification in the setting where it is known that the underlying partially-observed linear dynamical system lies within a finite collection of known candidate models. We first consider the problem of identification from a given trajectory, which in this setting reduces to identifying the index of the true model with high probability. We characterize the finite-time sample complexity of this problem by leveraging recent advances in the non-asymptotic analysis of linear least-square methods in the literature. In comparison to the earlier results that assume no prior knowledge of the system, our approach takes advantage of the smaller hypothesis class and leads to the design of a learner with a dimension-free sample complexity bound. Next, we consider the switching control of linear systems, where there is a candidate controller for each of the candidate models and data is collected through interaction of the system with a collection of potentially destabilizing controllers. We develop a dimension-dependent criterion that can detect those destabilizing controllers in finite time. By leveraging these results, we propose a data-driven switching strategy that identifies the unknown parameters of the underlying system. We then provide a non-asymptotic analysis of its performance and discuss its implications on the classical method of estimator-based supervisory control.

Private Synthetic Data Meets Ensemble Learning

When machine learning models are trained on synthetic data and then deployed on real data, there is often a performance drop due to the distribution shift between synthetic and real data. In this paper, we introduce a new ensemble strategy for training downstream models, with the goal of enhancing their performance when used on real data. We generate multiple synthetic datasets by applying a differential privacy (DP) mechanism several times in parallel and then ensemble the downstream models trained on these datasets. While each synthetic dataset might deviate more from the real data distribution, they collectively increase sample diversity. This may enhance the robustness of downstream models against distribution shifts. Our extensive experiments reveal that while ensembling does not enhance downstream performance (compared with training a single model) for models trained on synthetic data generated by marginal-based or workload-based DP mechanisms, our proposed ensemble strategy does improve the performance for models trained using GAN-based DP mechanisms in terms of both accuracy and calibration of downstream models.

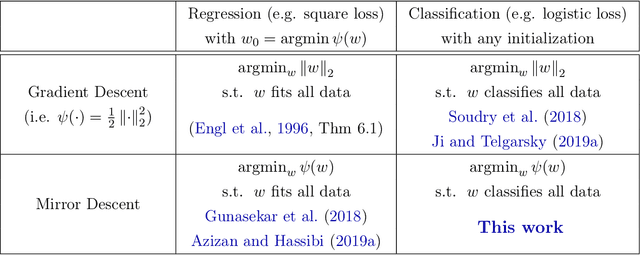
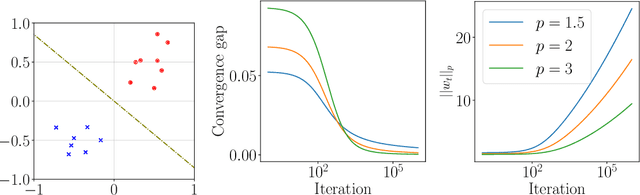
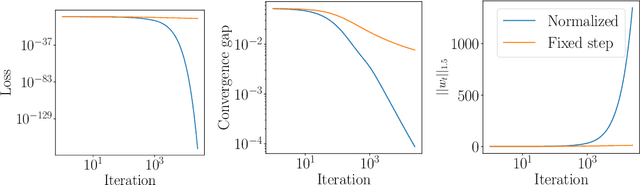
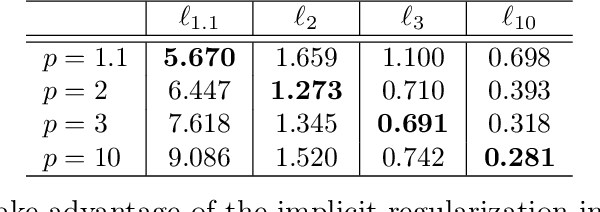
A Unified Approach to Controlling Implicit Regularization via Mirror Descent

Inspired by the remarkable success of deep neural networks, there has been significant interest in understanding the generalization performance of overparameterized models. Substantial efforts have been invested in characterizing how optimization algorithms impact generalization through their "preferred" solutions, a phenomenon commonly referred to as implicit regularization. In particular, it has been argued that gradient descent (GD) induces an implicit $\ell_2$-norm regularization in regression and classification problems. However, the implicit regularization of different algorithms are confined to either a specific geometry or a particular class of learning problems, indicating a gap in a general approach for controlling the implicit regularization. To address this, we present a unified approach using mirror descent (MD), a notable generalization of GD, to control implicit regularization in both regression and classification settings. More specifically, we show that MD with the general class of homogeneous potential functions converges in direction to a generalized maximum-margin solution for linear classification problems, thereby answering a long-standing question in the classification setting. Further, we show that MD can be implemented efficiently and under suitable conditions, enjoys fast convergence. Through comprehensive experiments, we demonstrate that MD is a versatile method to produce learned models with different regularizers, which in turn have different generalization performances.

Online Learning for Equilibrium Pricing in Markets under Incomplete Information

The study of market equilibria is central to economic theory, particularly in efficiently allocating scarce resources. However, the computation of equilibrium prices at which the supply of goods matches their demand typically relies on having access to complete information on private attributes of agents, e.g., suppliers' cost functions, which are often unavailable in practice. Motivated by this practical consideration, we consider the problem of setting equilibrium prices in the incomplete information setting wherein a market operator seeks to satisfy the customer demand for a commodity by purchasing the required amount from competing suppliers with privately known cost functions unknown to the market operator. In this incomplete information setting, we consider the online learning problem of learning equilibrium prices over time while jointly optimizing three performance metrics -- unmet demand, cost regret, and payment regret -- pertinent in the context of equilibrium pricing over a horizon of $T$ periods. We first consider the setting when suppliers' cost functions are fixed and develop algorithms that achieve a regret of $O(\log \log T)$ when the customer demand is constant over time, or $O(\sqrt{T} \log \log T)$ when the demand is variable over time. Next, we consider the setting when the suppliers' cost functions can vary over time and illustrate that no online algorithm can achieve sublinear regret on all three metrics when the market operator has no information about how the cost functions change over time. Thus, we consider an augmented setting wherein the operator has access to hints/contexts that, without revealing the complete specification of the cost functions, reflect the variation in the cost functions over time and propose an algorithm with sublinear regret in this augmented setting.