Online Learning for Equilibrium Pricing in Markets under Incomplete Information

The study of market equilibria is central to economic theory, particularly in efficiently allocating scarce resources. However, the computation of equilibrium prices at which the supply of goods matches their demand typically relies on having access to complete information on private attributes of agents, e.g., suppliers' cost functions, which are often unavailable in practice. Motivated by this practical consideration, we consider the problem of setting equilibrium prices in the incomplete information setting wherein a market operator seeks to satisfy the customer demand for a commodity by purchasing the required amount from competing suppliers with privately known cost functions unknown to the market operator. In this incomplete information setting, we consider the online learning problem of learning equilibrium prices over time while jointly optimizing three performance metrics -- unmet demand, cost regret, and payment regret -- pertinent in the context of equilibrium pricing over a horizon of $T$ periods. We first consider the setting when suppliers' cost functions are fixed and develop algorithms that achieve a regret of $O(\log \log T)$ when the customer demand is constant over time, or $O(\sqrt{T} \log \log T)$ when the demand is variable over time. Next, we consider the setting when the suppliers' cost functions can vary over time and illustrate that no online algorithm can achieve sublinear regret on all three metrics when the market operator has no information about how the cost functions change over time. Thus, we consider an augmented setting wherein the operator has access to hints/contexts that, without revealing the complete specification of the cost functions, reflect the variation in the cost functions over time and propose an algorithm with sublinear regret in this augmented setting.

Online Learning in Fisher Markets with Unknown Agent Preferences

In a Fisher market, agents (users) spend a budget of (artificial) currency to buy goods that maximize their utilities, and producers set prices on capacity-constrained goods such that the market clears. The equilibrium prices in such a market are typically computed through the solution of a convex program, e.g., the Eisenberg-Gale program, that aggregates users' preferences into a centralized social welfare objective. However, the computation of equilibrium prices using convex programs assumes that all transactions happen in a static market wherein all users are present simultaneously and relies on complete information on each user's budget and utility function. Since, in practice, information on users' utilities and budgets is unknown and users tend to arrive over time in the market, we study an online variant of Fisher markets, wherein users enter the market sequentially. We focus on the setting where users have linear utilities with privately known utility and budget parameters drawn i.i.d. from a distribution $\mathcal{D}$. In this setting, we develop a simple yet effective algorithm to set prices that preserves user privacy while achieving a regret and capacity violation of $O(\sqrt{n})$, where $n$ is the number of arriving users and the capacities of the goods scale as $O(n)$. Here, our regret measure represents the optimality gap in the objective of the Eisenberg-Gale program between the online allocation policy and that of an offline oracle with complete information on users' budgets and utilities. To establish the efficacy of our approach, we show that even an algorithm that sets expected equilibrium prices with perfect information on the distribution $\mathcal{D}$ cannot achieve both a regret and constraint violation of better than $\Omega(\sqrt{n})$. Finally, we present numerical experiments to demonstrate the performance of our approach relative to several benchmarks.

Online Learning for Traffic Routing under Unknown Preferences

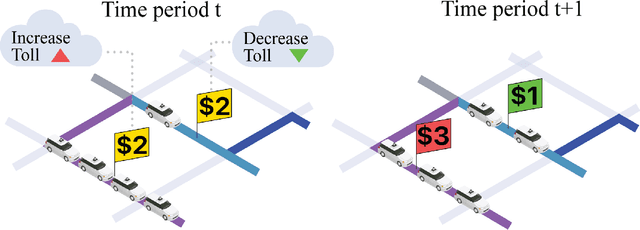
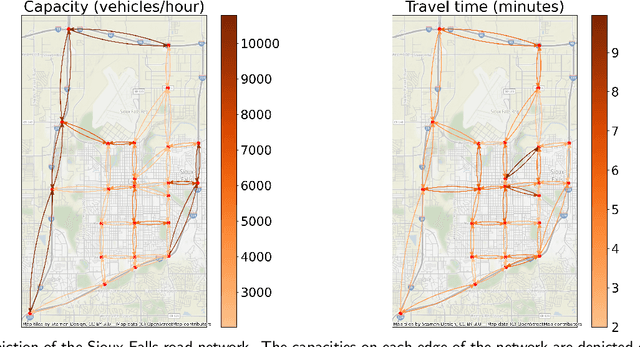
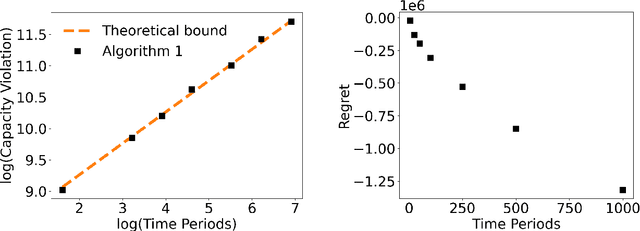
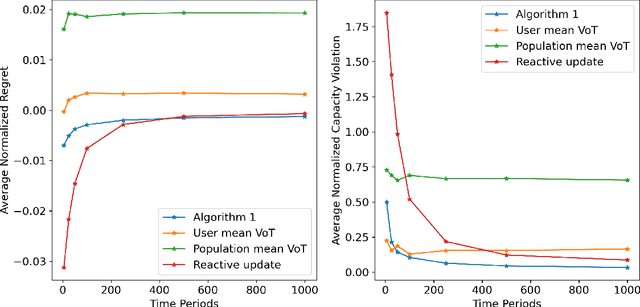
In transportation networks, users typically choose routes in a decentralized and self-interested manner to minimize their individual travel costs, which, in practice, often results in inefficient overall outcomes for society. As a result, there has been a growing interest in designing road tolling schemes to cope with these efficiency losses and steer users toward a system-efficient traffic pattern. However, the efficacy of road tolling schemes often relies on having access to complete information on users' trip attributes, such as their origin-destination (O-D) travel information and their values of time, which may not be available in practice. Motivated by this practical consideration, we propose an online learning approach to set tolls in a traffic network to drive heterogeneous users with different values of time toward a system-efficient traffic pattern. In particular, we develop a simple yet effective algorithm that adjusts tolls at each time period solely based on the observed aggregate flows on the roads of the network without relying on any additional trip attributes of users, thereby preserving user privacy. In the setting where the O-D pairs and values of time of users are drawn i.i.d. at each period, we show that our approach obtains an expected regret and road capacity violation of $O(\sqrt{T})$, where $T$ is the number of periods over which tolls are updated. Our regret guarantee is relative to an offline oracle that has complete information on users' trip attributes. We further establish a $\Omega(\sqrt{T})$ lower bound on the regret of any algorithm, which establishes that our algorithm is optimal up to constants. Finally, we demonstrate the superior performance of our approach relative to several benchmarks on a real-world transportation network, thereby highlighting its practical applicability.