Multiple regression techniques for modeling dates of first performances of Shakespeare-era plays

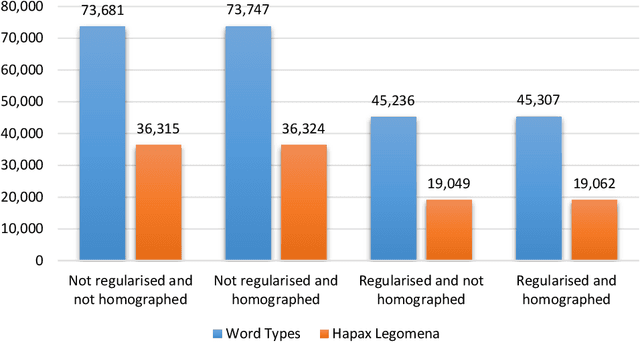
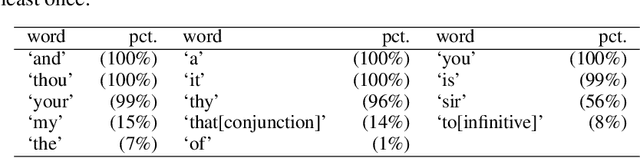
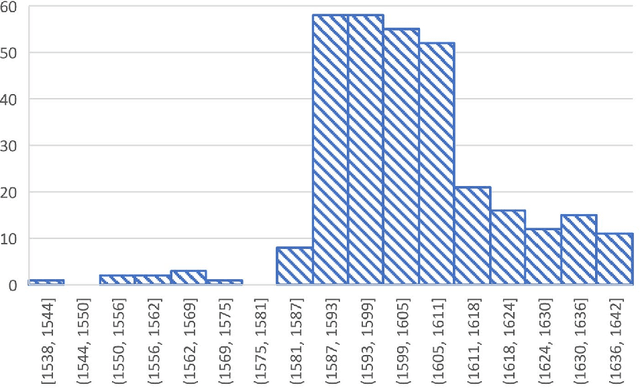
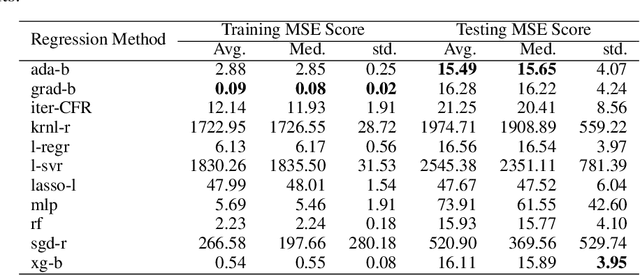
The date of the first performance of a play of Shakespeare's time must usually be guessed with reference to multiple indirect external sources, or to some aspect of the content or style of the play. Identifying these dates is important to literary history and to accounts of developing authorial styles, such as Shakespeare's. In this study, we took a set of Shakespeare-era plays (181 plays from the period 1585--1610), added the best-guess dates for them from a standard reference work as metadata, and calculated a set of probabilities of individual words in these samples. We applied 11 regression methods to predict the dates of the plays at an 80/20 training/test split. We withdrew one play at a time, used the best-guess date metadata with the probabilities and weightings to infer its date, and thus built a model of date-probabilities interaction. We introduced a memetic algorithm-based Continued Fraction Regression (CFR) which delivered models using a small number of variables, leading to an interpretable model and reduced dimensionality. An in-depth analysis of the most commonly occurring 20 words in the CFR models in 100 independent runs helps explain the trends in linguistic and stylistic terms. The analysis with the subset of words revealed an interesting correlation of signature words with the Shakespeare-era play's genre.

Learning to extrapolate using continued fractions: Predicting the critical temperature of superconductor materials

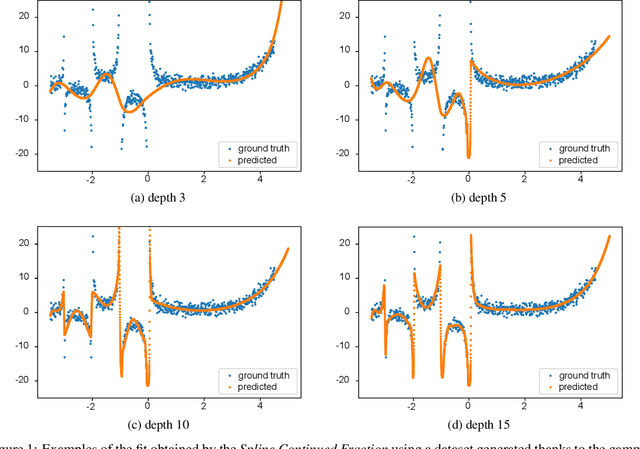
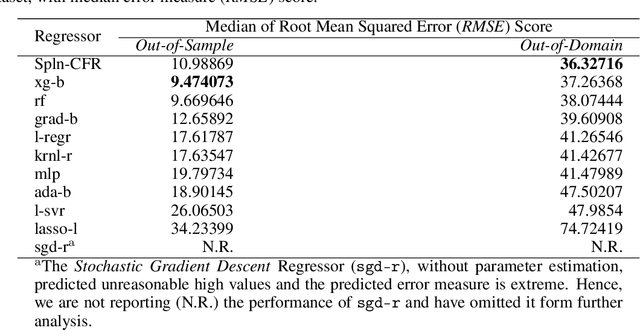
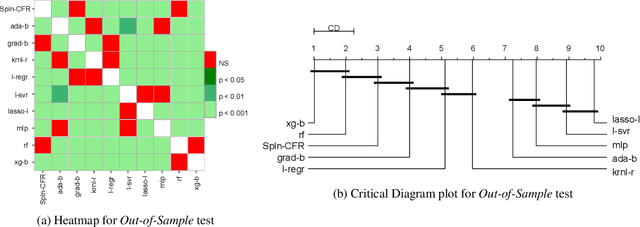
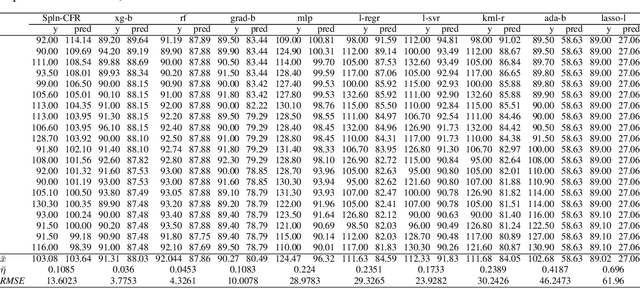
In Artificial Intelligence we often seek to identify an unknown target function of many variables $y=f(\mathbf{x})$ giving a limited set of instances $S=\{(\mathbf{x^{(i)}},y^{(i)})\}$ with $\mathbf{x^{(i)}} \in D$ where $D$ is a domain of interest. We refer to $S$ as the training set and the final quest is to identify the mathematical model that approximates this target function for new $\mathbf{x}$; with the set $T=\{ \mathbf{x^{(j)}} \} \subset D$ with $T \neq S$ (i.e. thus testing the model generalisation). However, for some applications, the main interest is approximating well the unknown function on a larger domain $D'$ that contains $D$. In cases involving the design of new structures, for instance, we may be interested in maximizing $f$; thus, the model derived from $S$ alone should also generalize well in $D'$ for samples with values of $y$ larger than the largest observed in $S$. In that sense, the AI system would provide important information that could guide the design process, e.g., using the learned model as a surrogate function to design new lab experiments. We introduce a method for multivariate regression based on iterative fitting of a continued fraction by incorporating additive spline models. We compared it with established methods such as AdaBoost, Kernel Ridge, Linear Regression, Lasso Lars, Linear Support Vector Regression, Multi-Layer Perceptrons, Random Forests, Stochastic Gradient Descent and XGBoost. We tested the performance on the important problem of predicting the critical temperature of superconductors based on physical-chemical characteristics.

Analytic Continued Fractions for Regression: A Memetic Algorithm Approach

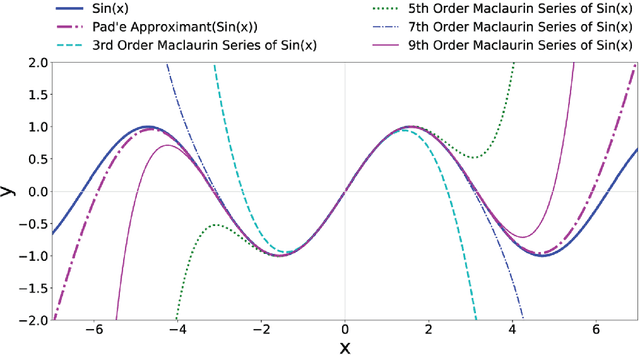
We present an approach for regression problems that employs analytic continued fractions as a novel representation. Comparative computational results using a memetic algorithm are reported in this work. Our experiments included fifteen other different machine learning approaches including five genetic programming methods for symbolic regression and ten machine learning methods. The comparison on training and test generalization was performed using 94 datasets of the Penn State Machine Learning Benchmark. The statistical tests showed that the generalization results using analytic continued fractions provides a powerful and interesting new alternative in the quest for compact and interpretable mathematical models for artificial intelligence.

mQAPViz: A divide-and-conquer multi-objective optimization algorithm to compute large data visualizations

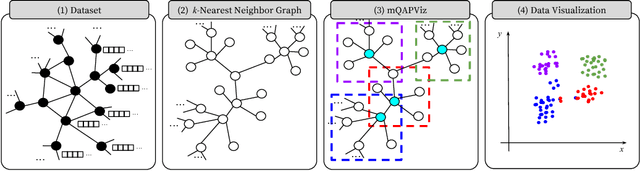
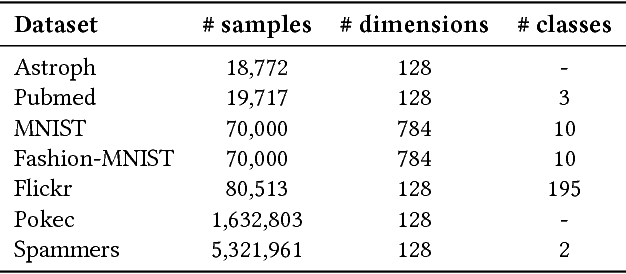
Algorithms for data visualizations are essential tools for transforming data into useful narratives. Unfortunately, very few visualization algorithms can handle the large datasets of many real-world scenarios. In this study, we address the visualization of these datasets as a Multi-Objective Optimization Problem. We propose mQAPViz, a divide-and-conquer multi-objective optimization algorithm to compute large-scale data visualizations. Our method employs the Multi-Objective Quadratic Assignment Problem (mQAP) as the mathematical foundation to solve the visualization task at hand. The algorithm applies advanced sampling techniques originating from the field of machine learning and efficient data structures to scale to millions of data objects. The algorithm allocates objects onto a 2D grid layout. Experimental results on real-world and large datasets demonstrate that mQAPViz is a competitive alternative to existing techniques.

Target Curricula via Selection of Minimum Feature Sets: a Case Study in Boolean Networks

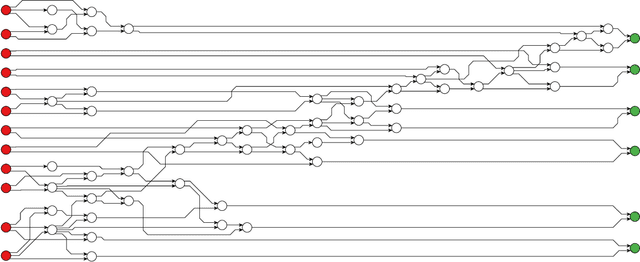
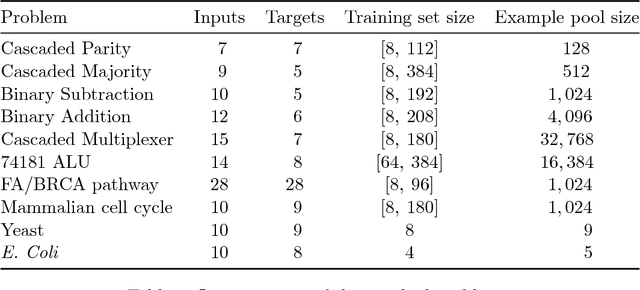
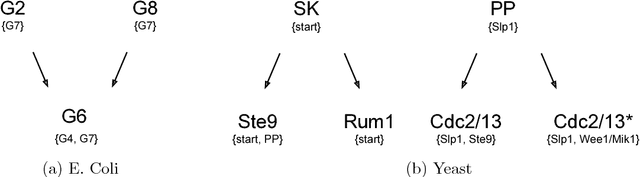
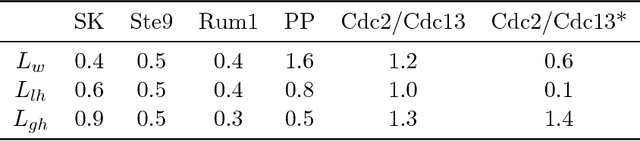
We consider the effect of introducing a curriculum of targets when training Boolean models on supervised Multi Label Classification (MLC) problems. In particular, we consider how to order targets in the absence of prior knowledge, and how such a curriculum may be enforced when using meta-heuristics to train discrete non-linear models. We show that hierarchical dependencies between targets can be exploited by enforcing an appropriate curriculum using hierarchical loss functions. On several multi output circuit-inference problems with known target difficulties, Feedforward Boolean Networks (FBNs) trained with such a loss function achieve significantly lower out-of-sample error, up to $10\%$ in some cases. This improvement increases as the loss places more emphasis on target order and is strongly correlated with an easy-to-hard curricula. We also demonstrate the same improvements on three real-world models and two Gene Regulatory Network (GRN) inference problems. We posit a simple a-priori method for identifying an appropriate target order and estimating the strength of target relationships in Boolean MLCs. These methods use intrinsic dimension as a proxy for target difficulty, which is estimated using optimal solutions to a combinatorial optimisation problem known as the Minimum-Feature-Set (minFS) problem. We also demonstrate that the same generalisation gains can be achieved without providing any knowledge of target difficulty.

PasMoQAP: A Parallel Asynchronous Memetic Algorithm for solving the Multi-Objective Quadratic Assignment Problem

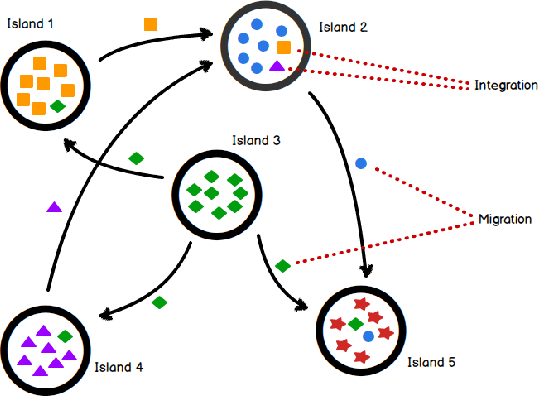
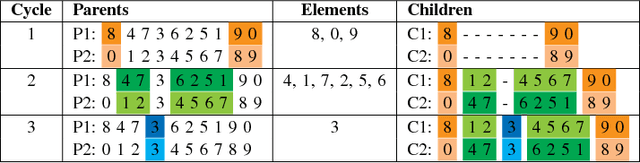
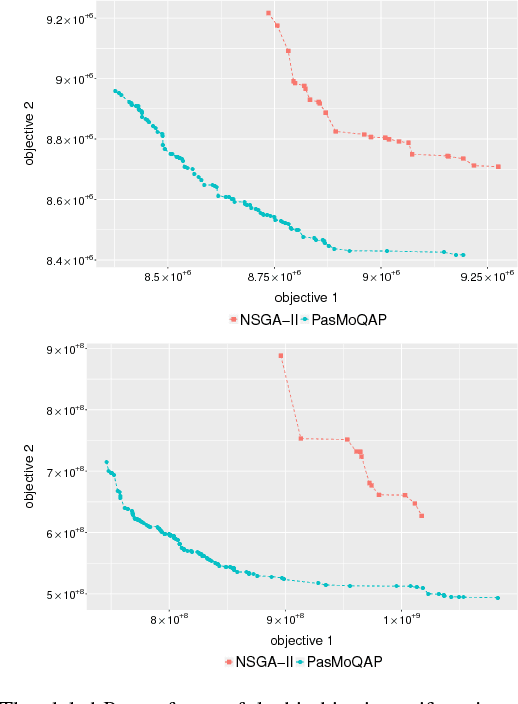
Multi-Objective Optimization Problems (MOPs) have attracted growing attention during the last decades. Multi-Objective Evolutionary Algorithms (MOEAs) have been extensively used to address MOPs because are able to approximate a set of non-dominated high-quality solutions. The Multi-Objective Quadratic Assignment Problem (mQAP) is a MOP. The mQAP is a generalization of the classical QAP which has been extensively studied, and used in several real-life applications. The mQAP is defined as having as input several flows between the facilities which generate multiple cost functions that must be optimized simultaneously. In this study, we propose PasMoQAP, a parallel asynchronous memetic algorithm to solve the Multi-Objective Quadratic Assignment Problem. PasMoQAP is based on an island model that structures the population by creating sub-populations. The memetic algorithm on each island individually evolve a reduced population of solutions, and they asynchronously cooperate by sending selected solutions to the neighboring islands. The experimental results show that our approach significatively outperforms all the island-based variants of the multi-objective evolutionary algorithm NSGA-II. We show that PasMoQAP is a suitable alternative to solve the Multi-Objective Quadratic Assignment Problem.

Separating Sets of Strings by Finding Matching Patterns is Almost Always Hard

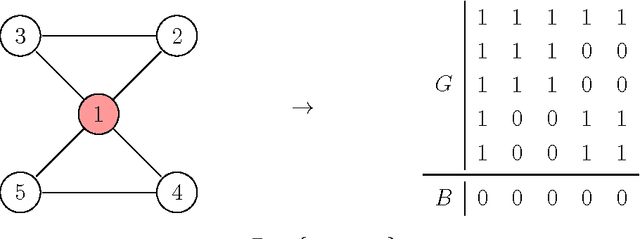
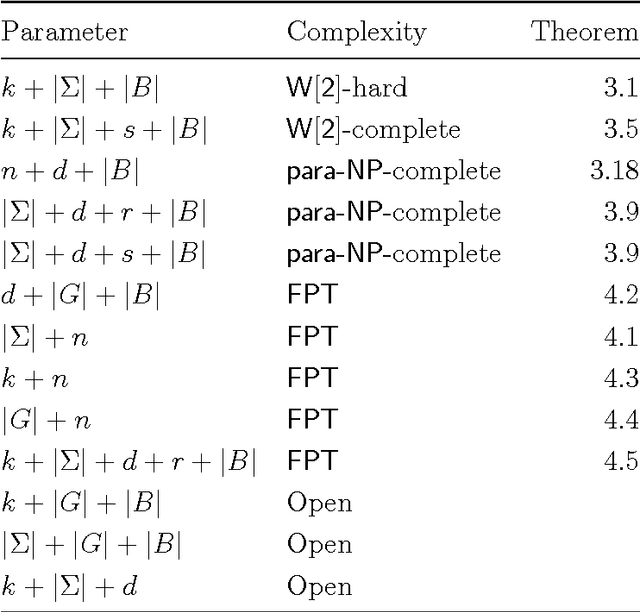
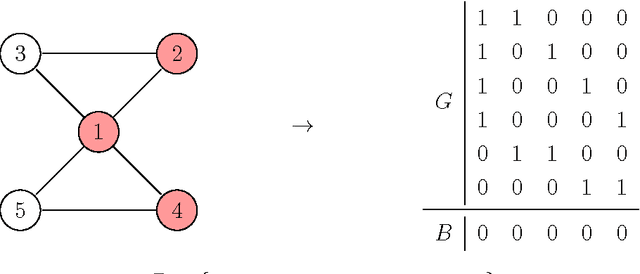
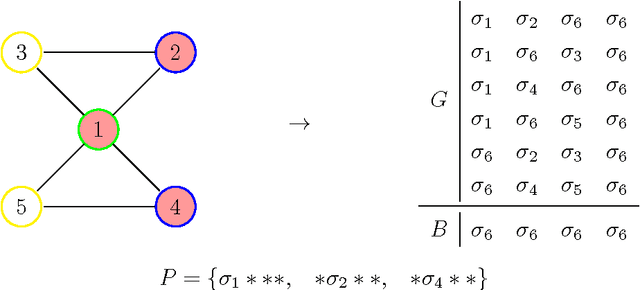
We study the complexity of the problem of searching for a set of patterns that separate two given sets of strings. This problem has applications in a wide variety of areas, most notably in data mining, computational biology, and in understanding the complexity of genetic algorithms. We show that the basic problem of finding a small set of patterns that match one set of strings but do not match any string in a second set is difficult (NP-complete, W[2]-hard when parameterized by the size of the pattern set, and APX-hard). We then perform a detailed parameterized analysis of the problem, separating tractable and intractable variants. In particular we show that parameterizing by the size of pattern set and the number of strings, and the size of the alphabet and the number of strings give FPT results, amongst others.