Multiple regression techniques for modeling dates of first performances of Shakespeare-era plays

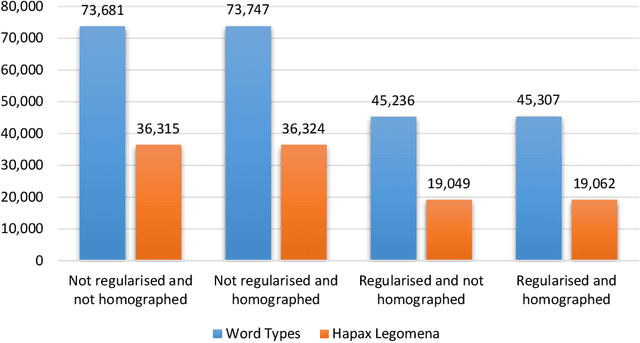
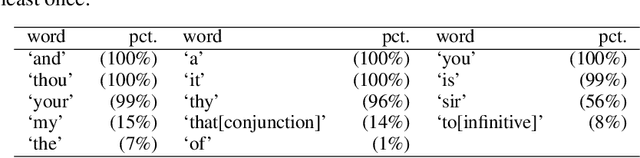
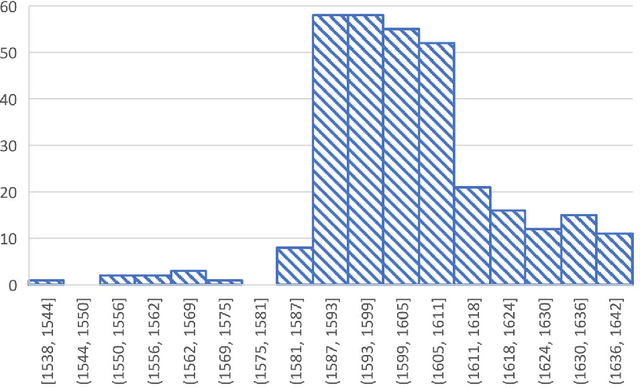
The date of the first performance of a play of Shakespeare's time must usually be guessed with reference to multiple indirect external sources, or to some aspect of the content or style of the play. Identifying these dates is important to literary history and to accounts of developing authorial styles, such as Shakespeare's. In this study, we took a set of Shakespeare-era plays (181 plays from the period 1585--1610), added the best-guess dates for them from a standard reference work as metadata, and calculated a set of probabilities of individual words in these samples. We applied 11 regression methods to predict the dates of the plays at an 80/20 training/test split. We withdrew one play at a time, used the best-guess date metadata with the probabilities and weightings to infer its date, and thus built a model of date-probabilities interaction. We introduced a memetic algorithm-based Continued Fraction Regression (CFR) which delivered models using a small number of variables, leading to an interpretable model and reduced dimensionality. An in-depth analysis of the most commonly occurring 20 words in the CFR models in 100 independent runs helps explain the trends in linguistic and stylistic terms. The analysis with the subset of words revealed an interesting correlation of signature words with the Shakespeare-era play's genre.

Learning to extrapolate using continued fractions: Predicting the critical temperature of superconductor materials

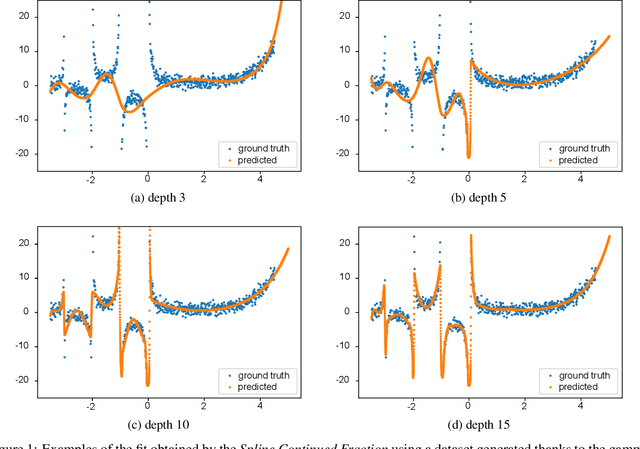
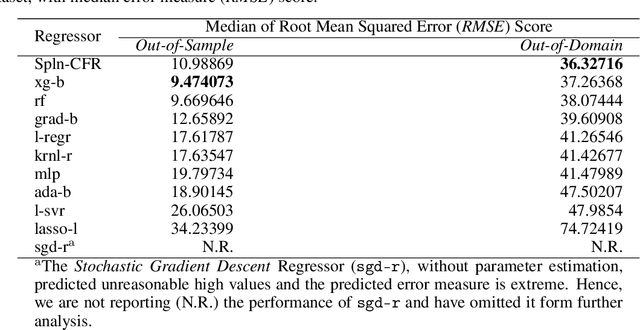
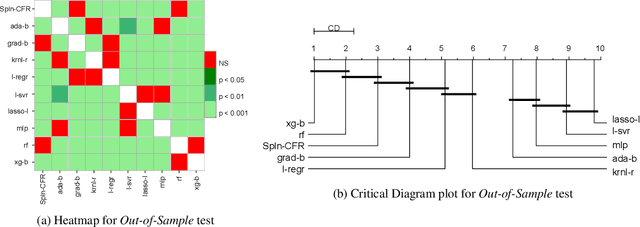
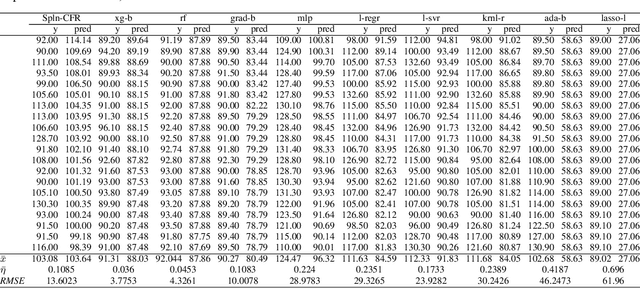
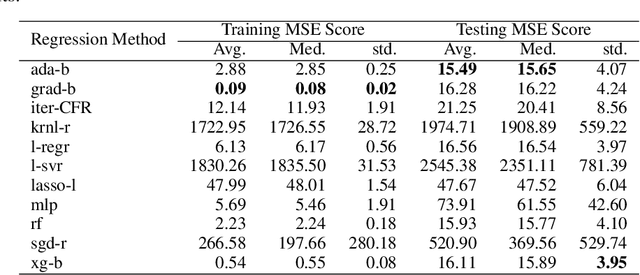
In Artificial Intelligence we often seek to identify an unknown target function of many variables $y=f(\mathbf{x})$ giving a limited set of instances $S=\{(\mathbf{x^{(i)}},y^{(i)})\}$ with $\mathbf{x^{(i)}} \in D$ where $D$ is a domain of interest. We refer to $S$ as the training set and the final quest is to identify the mathematical model that approximates this target function for new $\mathbf{x}$; with the set $T=\{ \mathbf{x^{(j)}} \} \subset D$ with $T \neq S$ (i.e. thus testing the model generalisation). However, for some applications, the main interest is approximating well the unknown function on a larger domain $D'$ that contains $D$. In cases involving the design of new structures, for instance, we may be interested in maximizing $f$; thus, the model derived from $S$ alone should also generalize well in $D'$ for samples with values of $y$ larger than the largest observed in $S$. In that sense, the AI system would provide important information that could guide the design process, e.g., using the learned model as a surrogate function to design new lab experiments. We introduce a method for multivariate regression based on iterative fitting of a continued fraction by incorporating additive spline models. We compared it with established methods such as AdaBoost, Kernel Ridge, Linear Regression, Lasso Lars, Linear Support Vector Regression, Multi-Layer Perceptrons, Random Forests, Stochastic Gradient Descent and XGBoost. We tested the performance on the important problem of predicting the critical temperature of superconductors based on physical-chemical characteristics.