Learning to extrapolate using continued fractions: Predicting the critical temperature of superconductor materials
Paper and Code
Nov 27, 2020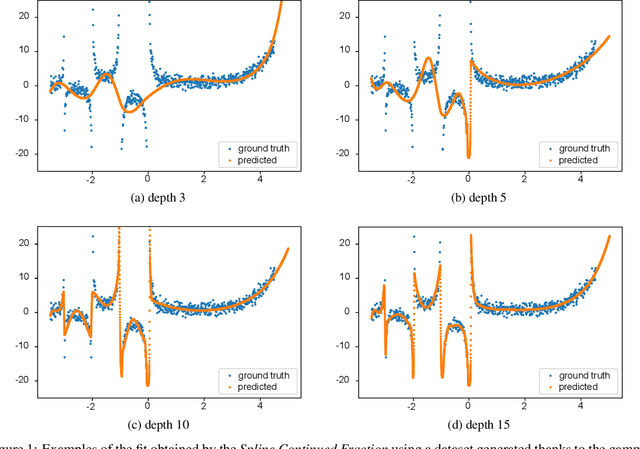
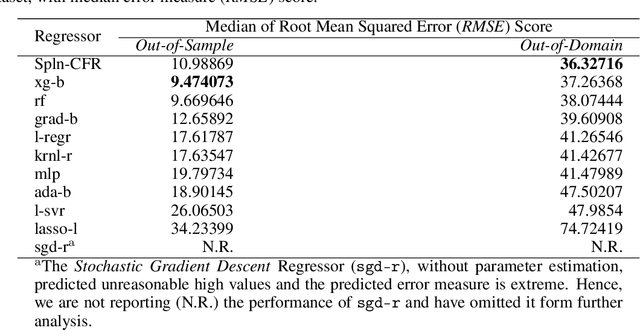
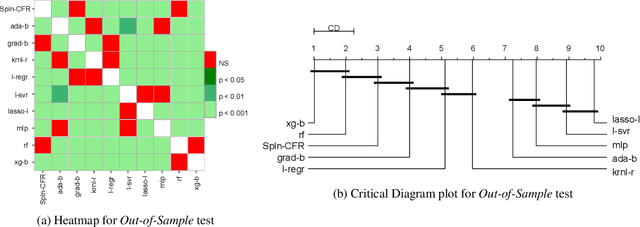
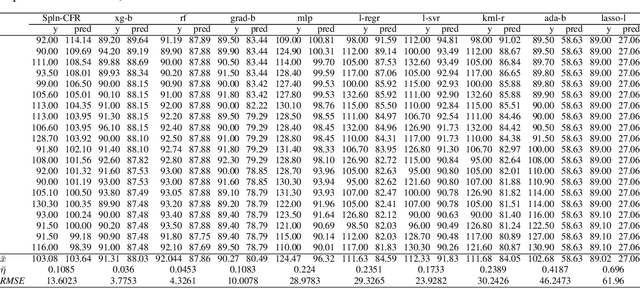
In Artificial Intelligence we often seek to identify an unknown target function of many variables $y=f(\mathbf{x})$ giving a limited set of instances $S=\{(\mathbf{x^{(i)}},y^{(i)})\}$ with $\mathbf{x^{(i)}} \in D$ where $D$ is a domain of interest. We refer to $S$ as the training set and the final quest is to identify the mathematical model that approximates this target function for new $\mathbf{x}$; with the set $T=\{ \mathbf{x^{(j)}} \} \subset D$ with $T \neq S$ (i.e. thus testing the model generalisation). However, for some applications, the main interest is approximating well the unknown function on a larger domain $D'$ that contains $D$. In cases involving the design of new structures, for instance, we may be interested in maximizing $f$; thus, the model derived from $S$ alone should also generalize well in $D'$ for samples with values of $y$ larger than the largest observed in $S$. In that sense, the AI system would provide important information that could guide the design process, e.g., using the learned model as a surrogate function to design new lab experiments. We introduce a method for multivariate regression based on iterative fitting of a continued fraction by incorporating additive spline models. We compared it with established methods such as AdaBoost, Kernel Ridge, Linear Regression, Lasso Lars, Linear Support Vector Regression, Multi-Layer Perceptrons, Random Forests, Stochastic Gradient Descent and XGBoost. We tested the performance on the important problem of predicting the critical temperature of superconductors based on physical-chemical characteristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge