Ariadne and Theseus: Exploration and Rendezvous with Two Mobile Agents in an Unknown Graph

We investigate two fundamental problems in mobile computing: exploration and rendezvous, with two distinct mobile agents in an unknown graph. The agents can read and write information on whiteboards that are located at all nodes. They both move along one adjacent edge at every time-step. In the exploration problem, both agents start from the same node of the graph and must traverse all of its edges. We show that a simple variant of depth-first search achieves collective exploration in $m$ synchronous time-steps, where $m$ is the number of edges of the graph. This improves the competitive ratio of collective graph exploration. In the rendezvous problem, the agents start from different nodes of the graph and must meet as fast as possible. We introduce an algorithm guaranteeing rendezvous in at most $\frac{3}{2}m$ time-steps. This improves over the so-called `wait for Mommy' algorithm which requires $2m$ time-steps. All our guarantees are derived from a more general asynchronous setting in which the speeds of the agents are controlled by an adversary at all times. Our guarantees also generalize to weighted graphs, if the number of edges $m$ is replaced by the sum of all edge lengths.

Gradient Descent for Low-Rank Functions

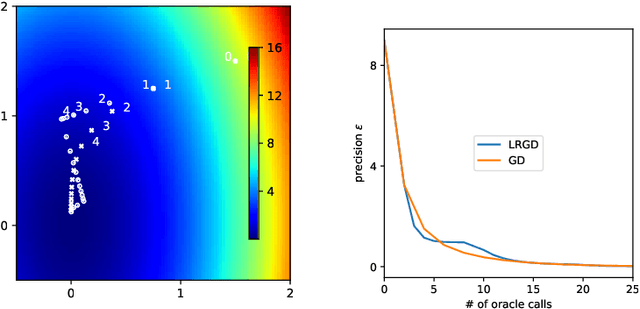
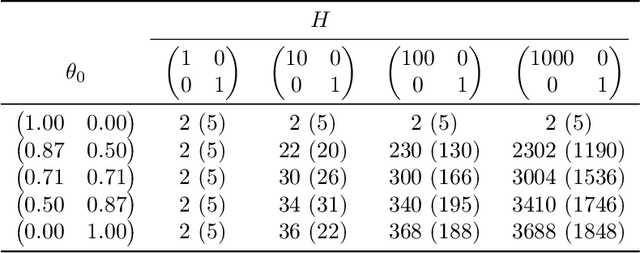
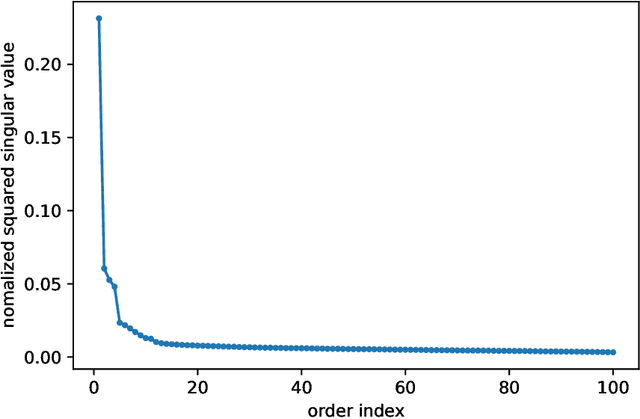
Several recent empirical studies demonstrate that important machine learning tasks, e.g., training deep neural networks, exhibit low-rank structure, where the loss function varies significantly in only a few directions of the input space. In this paper, we leverage such low-rank structure to reduce the high computational cost of canonical gradient-based methods such as gradient descent (GD). Our proposed \emph{Low-Rank Gradient Descent} (LRGD) algorithm finds an $\epsilon$-approximate stationary point of a $p$-dimensional function by first identifying $r \leq p$ significant directions, and then estimating the true $p$-dimensional gradient at every iteration by computing directional derivatives only along those $r$ directions. We establish that the "directional oracle complexities" of LRGD for strongly convex and non-convex objective functions are $\mathcal{O}(r \log(1/\epsilon) + rp)$ and $\mathcal{O}(r/\epsilon^2 + rp)$, respectively. When $r \ll p$, these complexities are smaller than the known complexities of $\mathcal{O}(p \log(1/\epsilon))$ and $\mathcal{O}(p/\epsilon^2)$ of {\gd} in the strongly convex and non-convex settings, respectively. Thus, LRGD significantly reduces the computational cost of gradient-based methods for sufficiently low-rank functions. In the course of our analysis, we also formally define and characterize the classes of exact and approximately low-rank functions.

Universal Online Learning with Unbounded Losses: Memory Is All You Need

We resolve an open problem of Hanneke on the subject of universally consistent online learning with non-i.i.d. processes and unbounded losses. The notion of an optimistically universal learning rule was defined by Hanneke in an effort to study learning theory under minimal assumptions. A given learning rule is said to be optimistically universal if it achieves a low long-run average loss whenever the data generating process makes this goal achievable by some learning rule. Hanneke posed as an open problem whether, for every unbounded loss, the family of processes admitting universal learning are precisely those having a finite number of distinct values almost surely. In this paper, we completely resolve this problem, showing that this is indeed the case. As a consequence, this also offers a dramatically simpler formulation of an optimistically universal learning rule for any unbounded loss: namely, the simple memorization rule already suffices. Our proof relies on constructing random measurable partitions of the instance space and could be of independent interest for solving other open questions. We extend the results to the non-realizable setting thereby providing an optimistically universal Bayes consistent learning rule.

Universal Online Learning with Bounded Loss: Reduction to Binary Classification

We study universal consistency of non-i.i.d. processes in the context of online learning. A stochastic process is said to admit universal consistency if there exists a learner that achieves vanishing average loss for any measurable response function on this process. When the loss function is unbounded, Blanchard et al. showed that the only processes admitting strong universal consistency are those taking a finite number of values almost surely. However, when the loss function is bounded, the class of processes admitting strong universal consistency is much richer and its characterization could be dependent on the response setting (Hanneke). In this paper, we show that this class of processes is independent from the response setting thereby closing an open question (Hanneke, Open Problem 3). Specifically, we show that the class of processes that admit universal online learning is the same for binary classification as for multiclass classification with countable number of classes. Consequently, any output setting with bounded loss can be reduced to binary classification. Our reduction is constructive and practical. Indeed, we show that the nearest neighbor algorithm is transported by our construction. For binary classification on a process admitting strong universal learning, we prove that nearest neighbor successfully learns at least all finite unions of intervals.

Approximating the Log-Partition Function

Variational approximation, such as mean-field (MF) and tree-reweighted (TRW), provide a computationally efficient approximation of the log-partition function for a generic graphical model. TRW provably provides an upper bound, but the approximation ratio is generally not quantified. As the primary contribution of this work, we provide an approach to quantify the approximation ratio through the property of the underlying graph structure. Specifically, we argue that (a variant of) TRW produces an estimate that is within factor $\frac{1}{\sqrt{\kappa(G)}}$ of the true log-partition function for any discrete pairwise graphical model over graph $G$, where $\kappa(G) \in (0,1]$ captures how far $G$ is from tree structure with $\kappa(G) = 1$ for trees and $2/N$ for the complete graph over $N$ vertices. As a consequence, the approximation ratio is $1$ for trees, $\sqrt{(d+1)/2}$ for any graph with maximum average degree $d$, and $\stackrel{\beta\to\infty}{\approx} 1+1/(2\beta)$ for graphs with girth (shortest cycle) at least $\beta \log N$. In general, $\kappa(G)$ is the solution of a max-min problem associated with $G$ that can be evaluated in polynomial time for any graph. Using samples from the uniform distribution over the spanning trees of G, we provide a near linear-time variant that achieves an approximation ratio equal to the inverse of square-root of minimal (across edges) effective resistance of the graph. We connect our results to the graph partition-based approximation method and thus provide a unified perspective. Keywords: variational inference, log-partition function, spanning tree polytope, minimum effective resistance, min-max spanning tree, local inference

Synthetic Interventions

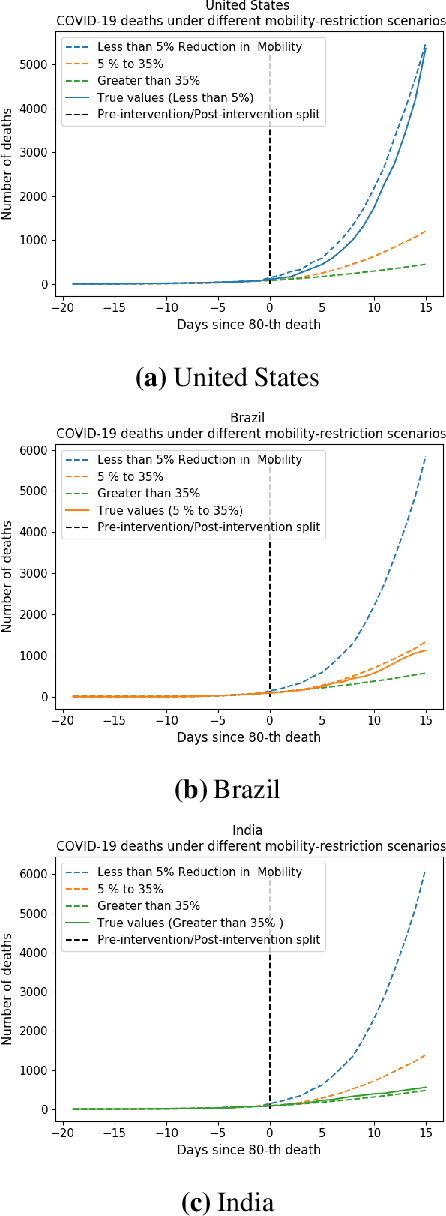
We develop a method to help quantify the impact different levels of mobility restrictions could have had on COVID-19 related deaths across nations. Synthetic control (SC) has emerged as a standard tool in such scenarios to produce counterfactual estimates if a particular intervention had not occurred, using just observational data. However, it remains an important open problem of how to extend SC to obtain counterfactual estimates if a particular intervention had occurred - this is exactly the question of the impact of mobility restrictions stated above. As our main contribution, we introduce synthetic interventions (SI), which helps resolve this open problem by allowing one to produce counterfactual estimates if there are multiple interventions of interest. We prove SI produces consistent counterfactual estimates under a tensor factor model. Our finite sample analysis shows the test error decays as $1/T_0$, where $T_0$ is the amount of observed pre-intervention data. As a special case, this improves upon the $1/\sqrt{T_0}$ bound on test error for SC in prior works. Our test error bound holds under a certain "subspace inclusion" condition; we furnish a data-driven hypothesis test with provable guarantees to check for this condition. This also provides a quantitative hypothesis test for when to use SC, currently absent in the literature. Technically, we establish the parameter estimation and test error for Principal Component Regression (a key subroutine in SI and several SC variants) under the setting of error-in-variable regression decays as $1/T_0$, where $T_0$ is the number of samples observed; this improves the best prior test error bound of $1/\sqrt{T_0}$. In addition to the COVID-19 case study, we show how SI can be used to run data-efficient, personalized randomized control trials using real data from a large e-commerce website and a large developmental economics study.