Gradient Descent is Pareto-Optimal in the Oracle Complexity and Memory Tradeoff for Feasibility Problems

In this paper we provide oracle complexity lower bounds for finding a point in a given set using a memory-constrained algorithm that has access to a separation oracle. We assume that the set is contained within the unit $d$-dimensional ball and contains a ball of known radius $\epsilon>0$. This setup is commonly referred to as the feasibility problem. We show that to solve feasibility problems with accuracy $\epsilon \geq e^{-d^{o(1)}}$, any deterministic algorithm either uses $d^{1+\delta}$ bits of memory or must make at least $1/(d^{0.01\delta }\epsilon^{2\frac{1-\delta}{1+1.01 \delta}-o(1)})$ oracle queries, for any $\delta\in[0,1]$. Additionally, we show that randomized algorithms either use $d^{1+\delta}$ memory or make at least $1/(d^{2\delta} \epsilon^{2(1-4\delta)-o(1)})$ queries for any $\delta\in[0,\frac{1}{4}]$. Because gradient descent only uses linear memory $\mathcal O(d\ln 1/\epsilon)$ but makes $\Omega(1/\epsilon^2)$ queries, our results imply that it is Pareto-optimal in the oracle complexity/memory tradeoff. Further, our results show that the oracle complexity for deterministic algorithms is always polynomial in $1/\epsilon$ if the algorithm has less than quadratic memory in $d$. This reveals a sharp phase transition since with quadratic $\mathcal O(d^2 \ln1/\epsilon)$ memory, cutting plane methods only require $\mathcal O(d\ln 1/\epsilon)$ queries.

Non-stationary Contextual Bandits and Universal Learning

We study the fundamental limits of learning in contextual bandits, where a learner's rewards depend on their actions and a known context, which extends the canonical multi-armed bandit to the case where side-information is available. We are interested in universally consistent algorithms, which achieve sublinear regret compared to any measurable fixed policy, without any function class restriction. For stationary contextual bandits, when the underlying reward mechanism is time-invariant, [Blanchard et al.] characterized learnable context processes for which universal consistency is achievable; and further gave algorithms ensuring universal consistency whenever this is achievable, a property known as optimistic universal consistency. It is well understood, however, that reward mechanisms can evolve over time, possibly depending on the learner's actions. We show that optimistic universal learning for non-stationary contextual bandits is impossible in general, contrary to all previously studied settings in online learning -- including standard supervised learning. We also give necessary and sufficient conditions for universal learning under various non-stationarity models, including online and adversarial reward mechanisms. In particular, the set of learnable processes for non-stationary rewards is still extremely general -- larger than i.i.d., stationary or ergodic -- but in general strictly smaller than that for supervised learning or stationary contextual bandits, shedding light on new non-stationary phenomena.

Contextual Bandits and Optimistically Universal Learning

We consider the contextual bandit problem on general action and context spaces, where the learner's rewards depend on their selected actions and an observable context. This generalizes the standard multi-armed bandit to the case where side information is available, e.g., patients' records or customers' history, which allows for personalized treatment. We focus on consistency -- vanishing regret compared to the optimal policy -- and show that for large classes of non-i.i.d. contexts, consistency can be achieved regardless of the time-invariant reward mechanism, a property known as universal consistency. Precisely, we first give necessary and sufficient conditions on the context-generating process for universal consistency to be possible. Second, we show that there always exists an algorithm that guarantees universal consistency whenever this is achievable, called an optimistically universal learning rule. Interestingly, for finite action spaces, learnable processes for universal learning are exactly the same as in the full-feedback setting of supervised learning, previously studied in the literature. In other words, learning can be performed with partial feedback without any generalization cost. The algorithms balance a trade-off between generalization (similar to structural risk minimization) and personalization (tailoring actions to specific contexts). Lastly, we consider the case of added continuity assumptions on rewards and show that these lead to universal consistency for significantly larger classes of data-generating processes.

Universal Online Learning with Unbounded Losses: Memory Is All You Need

We resolve an open problem of Hanneke on the subject of universally consistent online learning with non-i.i.d. processes and unbounded losses. The notion of an optimistically universal learning rule was defined by Hanneke in an effort to study learning theory under minimal assumptions. A given learning rule is said to be optimistically universal if it achieves a low long-run average loss whenever the data generating process makes this goal achievable by some learning rule. Hanneke posed as an open problem whether, for every unbounded loss, the family of processes admitting universal learning are precisely those having a finite number of distinct values almost surely. In this paper, we completely resolve this problem, showing that this is indeed the case. As a consequence, this also offers a dramatically simpler formulation of an optimistically universal learning rule for any unbounded loss: namely, the simple memorization rule already suffices. Our proof relies on constructing random measurable partitions of the instance space and could be of independent interest for solving other open questions. We extend the results to the non-realizable setting thereby providing an optimistically universal Bayes consistent learning rule.

The Representation Power of Neural Networks: Breaking the Curse of Dimensionality

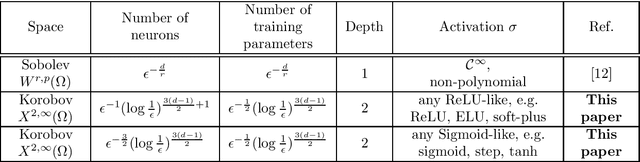
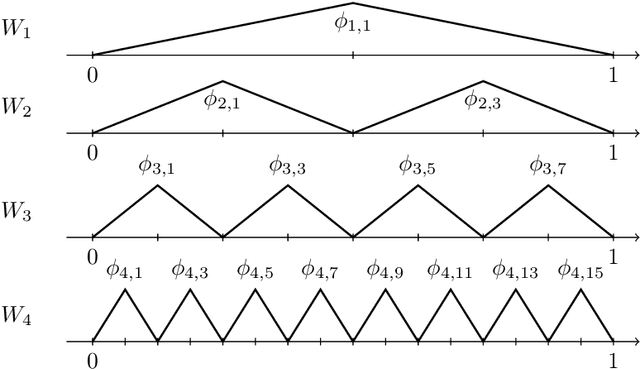
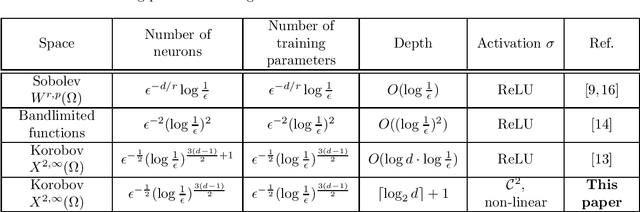
In this paper, we analyze the number of neurons and training parameters that a neural networks needs to approximate multivariate functions of bounded second mixed derivatives -- Korobov functions. We prove upper bounds on these quantities for shallow and deep neural networks, breaking the curse of dimensionality. Our bounds hold for general activation functions, including ReLU. We further prove that these bounds nearly match the minimal number of parameters any continuous function approximator needs to approximate Korobov functions, showing that neural networks are near-optimal function approximators.