Sharper Guarantees for Learning Neural Network Classifiers with Gradient Methods

In this paper, we study the data-dependent convergence and generalization behavior of gradient methods for neural networks with smooth activation. Our first result is a novel bound on the excess risk of deep networks trained by the logistic loss, via an alogirthmic stability analysis. Compared to previous works, our results improve upon the shortcomings of the well-established Rademacher complexity-based bounds. Importantly, the bounds we derive in this paper are tighter, hold even for neural networks of small width, do not scale unfavorably with width, are algorithm-dependent, and consequently capture the role of initialization on the sample complexity of gradient descent for deep nets. Specialized to noiseless data separable with margin $\gamma$ by neural tangent kernel (NTK) features of a network of width $\Omega(\poly(\log(n)))$, we show the test-error rate to be $e^{O(L)}/{\gamma^2 n}$, where $n$ is the training set size and $L$ denotes the number of hidden layers. This is an improvement in the test loss bound compared to previous works while maintaining the poly-logarithmic width conditions. We further investigate excess risk bounds for deep nets trained with noisy data, establishing that under a polynomial condition on the network width, gradient descent can achieve the optimal excess risk. Finally, we show that a large step-size significantly improves upon the NTK regime's results in classifying the XOR distribution. In particular, we show for a one-hidden-layer neural network of constant width $m$ with quadratic activation and standard Gaussian initialization that mini-batch SGD with linear sample complexity and with a large step-size $\eta=m$ reaches the perfect test accuracy after only $\ceil{\log(d)}$ iterations, where $d$ is the data dimension.

On the Optimization and Generalization of Multi-head Attention

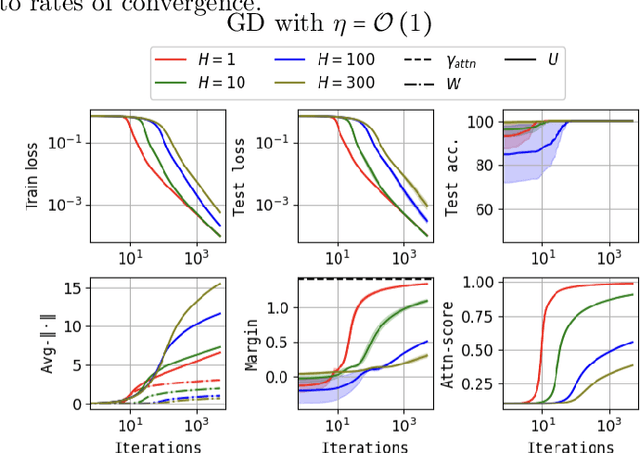
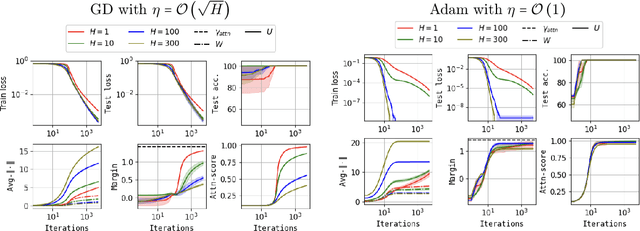
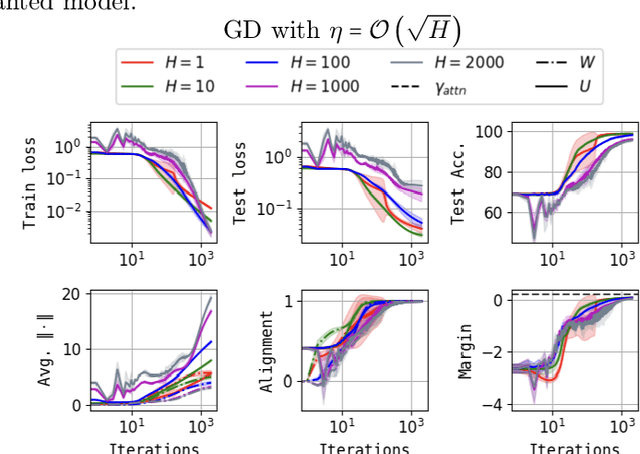
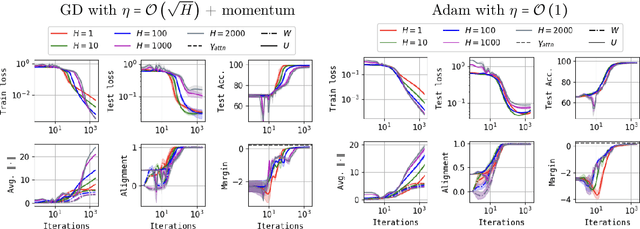
The training and generalization dynamics of the Transformer's core mechanism, namely the Attention mechanism, remain under-explored. Besides, existing analyses primarily focus on single-head attention. Inspired by the demonstrated benefits of overparameterization when training fully-connected networks, we investigate the potential optimization and generalization advantages of using multiple attention heads. Towards this goal, we derive convergence and generalization guarantees for gradient-descent training of a single-layer multi-head self-attention model, under a suitable realizability condition on the data. We then establish primitive conditions on the initialization that ensure realizability holds. Finally, we demonstrate that these conditions are satisfied for a simple tokenized-mixture model. We expect the analysis can be extended to various data-model and architecture variations.

Fast Convergence in Learning Two-Layer Neural Networks with Separable Data

Normalized gradient descent has shown substantial success in speeding up the convergence of exponentially-tailed loss functions (which includes exponential and logistic losses) on linear classifiers with separable data. In this paper, we go beyond linear models by studying normalized GD on two-layer neural nets. We prove for exponentially-tailed losses that using normalized GD leads to linear rate of convergence of the training loss to the global optimum. This is made possible by showing certain gradient self-boundedness conditions and a log-Lipschitzness property. We also study generalization of normalized GD for convex objectives via an algorithmic-stability analysis. In particular, we show that normalized GD does not overfit during training by establishing finite-time generalization bounds.

Generalization and Stability of Interpolating Neural Networks with Minimal Width

We investigate the generalization and optimization of $k$-homogeneous shallow neural-network classifiers in the interpolating regime. The study focuses on analyzing the performance of the model when it is capable of perfectly classifying the input data with a positive margin $\gamma$. When using gradient descent with logistic-loss minimization, we show that the training loss converges to zero at a rate of $\tilde O(1/\gamma^{2/k} T)$ given a polylogarithmic number of neurons. This suggests that gradient descent can find a perfect classifier for $n$ input data within $\tilde{\Omega}(n)$ iterations. Additionally, through a stability analysis we show that with $m=\Omega(\log^{4/k} (n))$ neurons and $T=\Omega(n)$ iterations, the test loss is bounded by $\tilde{O}(1/\gamma^{2/k} n)$. This is in contrast to existing stability results which require polynomial width and yield suboptimal generalization rates. Central to our analysis is the use of a new self-bounded weak convexity property, which leads to a generalized local quasi-convexity property for sufficiently parameterized neural-network classifiers. Eventually, despite the objective's non-convexity, this leads to convergence and generalization-gap bounds that are similar to those in the convex setting of linear logistic regression.

Decentralized Learning with Separable Data: Generalization and Fast Algorithms

Decentralized learning offers privacy and communication efficiency when data are naturally distributed among agents communicating over an underlying graph. Motivated by overparameterized learning settings, in which models are trained to zero training loss, we study algorithmic and generalization properties of decentralized learning with gradient descent on separable data. Specifically, for decentralized gradient descent (DGD) and a variety of loss functions that asymptote to zero at infinity (including exponential and logistic losses), we derive novel finite-time generalization bounds. This complements a long line of recent work that studies the generalization performance and the implicit bias of gradient descent over separable data, but has thus far been limited to centralized learning scenarios. Notably, our generalization bounds match in order their centralized counterparts. Critical behind this, and of independent interest, is establishing novel bounds on the training loss and the rate-of-consensus of DGD for a class of self-bounded losses. Finally, on the algorithmic front, we design improved gradient-based routines for decentralized learning with separable data and empirically demonstrate orders-of-magnitude of speed-up in terms of both training and generalization performance.

Asymptotic Behavior of Adversarial Training in Binary Classification

It is widely known that several machine learning models are susceptible to adversarial attacks i.e., small adversarial perturbations applied to data points causing the model to misclassify the data. Adversarial training using empirical risk minimization methods, is the state-of-the-art method for defense against adversarial attacks. Despite being successful, several problems in understanding generalization performance of adversarial training remain open. In this paper, we derive precise theoretical predictions for the performance of adversarial training in binary linear classification. We consider the modern high-dimensional regime where the dimension of data grows with the size of the training dataset at a constant ratio. Our results provide exact asymptotics for the performance of estimators obtained by adversarial training with $\ell_q$-norm bounded perturbations ($q \ge 1$) and for binary labels and Gaussian features. These sharp predictions enable us to explore the role of various factors including over-parametrization ratio, data model and attack budget on the performance of adversarial training.

Fundamental Limits of Ridge-Regularized Empirical Risk Minimization in High Dimensions

Empirical Risk Minimization (ERM) algorithms are widely used in a variety of estimation and prediction tasks in signal-processing and machine learning applications. Despite their popularity, a theory that explains their statistical properties in modern regimes where both the number of measurements and the number of unknown parameters is large is only recently emerging. In this paper, we characterize for the first time the fundamental limits on the statistical accuracy of convex ERM for inference in high-dimensional generalized linear models. For a stylized setting with Gaussian features and problem dimensions that grow large at a proportional rate, we start with sharp performance characterizations and then derive tight lower bounds on the estimation and prediction error that hold over a wide class of loss functions and for any value of the regularization parameter. Our precise analysis has several attributes. First, it leads to a recipe for optimally tuning the loss function and the regularization parameter. Second, it allows to precisely quantify the sub-optimality of popular heuristic choices: for instance, we show that optimally-tuned least-squares is (perhaps surprisingly) approximately optimal for standard logistic data, but the sub-optimality gap grows drastically as the signal strength increases. Third, we use the bounds to precisely assess the merits of ridge-regularization as a function of the over-parameterization ratio. Notably, our bounds are expressed in terms of the Fisher Information of random variables that are simple functions of the data distribution, thus making ties to corresponding bounds in classical statistics.

Sharp Asymptotics and Optimal Performance for Inference in Binary Models

We study convex empirical risk minimization for high-dimensional inference in binary models. Our first result sharply predicts the statistical performance of such estimators in the linear asymptotic regime under isotropic Gaussian features. Importantly, the predictions hold for a wide class of convex loss functions, which we exploit in order to prove a bound on the best achievable performance among them. Notably, we show that the proposed bound is tight for popular binary models (such as Signed, Logistic or Probit), by constructing appropriate loss functions that achieve it. More interestingly, for binary linear classification under the Logistic and Probit models, we prove that the performance of least-squares is no worse than 0.997 and 0.98 times the optimal one. Numerical simulations corroborate our theoretical findings and suggest they are accurate even for relatively small problem dimensions.

Quantized Push-sum for Gossip and Decentralized Optimization over Directed Graphs

We consider a decentralized stochastic learning problem where data points are distributed among computing nodes communicating over a directed graph. As the model size gets large, decentralized learning faces a major bottleneck that is the heavy communication load due to each node transmitting large messages (model updates) to its neighbors. To tackle this bottleneck, we propose the quantized decentralized stochastic learning algorithm over directed graphs that is based on the push-sum algorithm in decentralized consensus optimization. More importantly, we prove that our algorithm achieves the same convergence rates of the decentralized stochastic learning algorithm with exact-communication for both convex and non-convex losses. A key technical challenge of the work is to prove exact convergence of the proposed decentralized learning algorithm in the presence of quantization noise with unbounded variance over directed graphs. We provide numerical evaluations that corroborate our main theoretical results and illustrate significant speed-up compared to the exact-communication methods.

Sharp Guarantees for Solving Random Equations with One-Bit Information

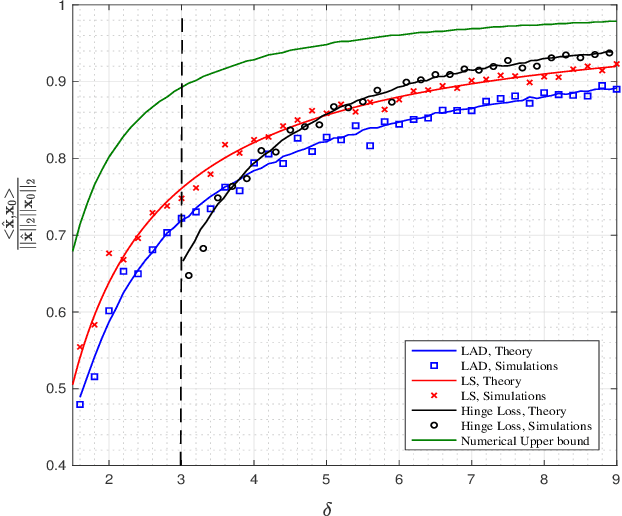
We study the performance of a wide class of convex optimization-based estimators for recovering a signal from corrupted one-bit measurements in high-dimensions. Our general result predicts sharply the performance of such estimators in the linear asymptotic regime when the measurement vectors have entries IID Gaussian. This includes, as a special case, the previously studied least-squares estimator and various novel results for other popular estimators such as least-absolute deviations, hinge-loss and logistic-loss. Importantly, we exploit the fact that our analysis holds for generic convex loss functions to prove a bound on the best achievable performance across the entire class of estimators. Numerical simulations corroborate our theoretical findings and suggest they are accurate even for relatively small problem dimensions.