Sharp Guarantees for Solving Random Equations with One-Bit Information
Paper and Code
Aug 12, 2019

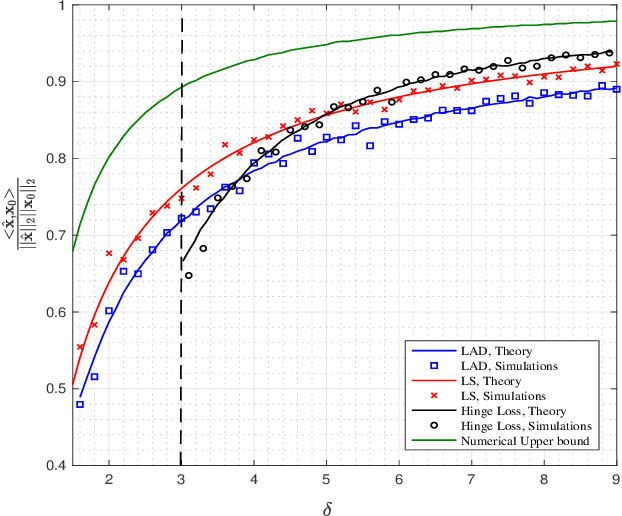

We study the performance of a wide class of convex optimization-based estimators for recovering a signal from corrupted one-bit measurements in high-dimensions. Our general result predicts sharply the performance of such estimators in the linear asymptotic regime when the measurement vectors have entries IID Gaussian. This includes, as a special case, the previously studied least-squares estimator and various novel results for other popular estimators such as least-absolute deviations, hinge-loss and logistic-loss. Importantly, we exploit the fact that our analysis holds for generic convex loss functions to prove a bound on the best achievable performance across the entire class of estimators. Numerical simulations corroborate our theoretical findings and suggest they are accurate even for relatively small problem dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge