Robust and Communication-Efficient Collaborative Learning
Paper and Code
Jul 24, 2019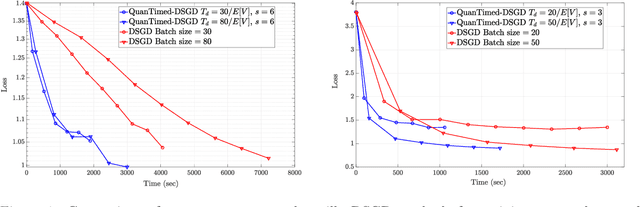
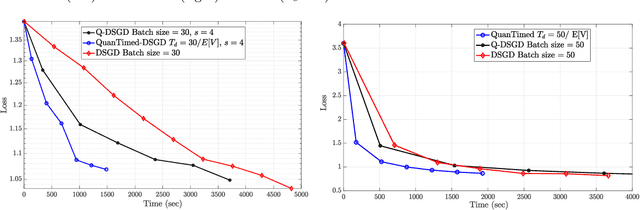
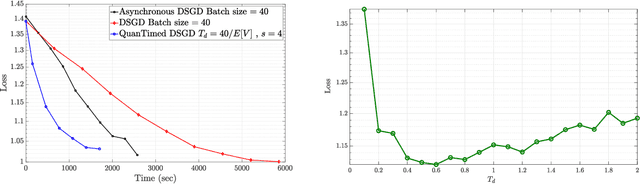
We consider a decentralized learning problem, where a set of computing nodes aim at solving a non-convex optimization problem collaboratively. It is well-known that decentralized optimization schemes face two major system bottlenecks: stragglers' delay and communication overhead. In this paper, we tackle these bottlenecks by proposing a novel decentralized and gradient-based optimization algorithm named as QuanTimed-DSGD. Our algorithm stands on two main ideas: (i) we impose a deadline on the local gradient computations of each node at each iteration of the algorithm, and (ii) the nodes exchange quantized versions of their local models. The first idea robustifies to straggling nodes and the second alleviates communication efficiency. The key technical contribution of our work is to prove that with non-vanishing noises for quantization and stochastic gradients, the proposed method exactly converges to the global optimal for convex loss functions, and finds a first-order stationary point in non-convex scenarios. Our numerical evaluations of the QuanTimed-DSGD on training benchmark datasets, MNIST and CIFAR-10, demonstrate speedups of up to 3x in run-time, compared to state-of-the-art decentralized optimization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge