Stamatios Lefkimmiatis
Speak, Edit, Repeat: High-Fidelity Voice Editing and Zero-Shot TTS with Cross-Attentive Mamba
Oct 06, 2025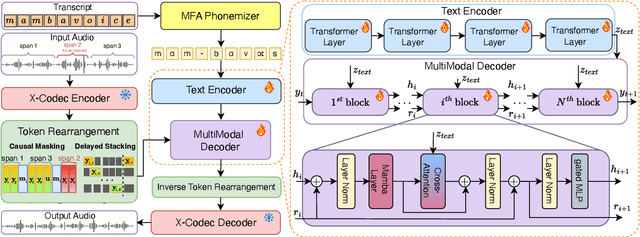
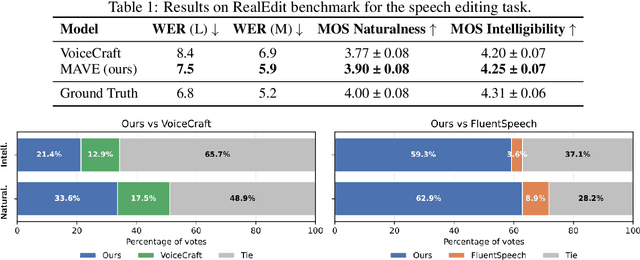


Abstract:We introduce MAVE (Mamba with Cross-Attention for Voice Editing and Synthesis), a novel autoregressive architecture for text-conditioned voice editing and high-fidelity text-to-speech (TTS) synthesis, built on a cross-attentive Mamba backbone. MAVE achieves state-of-the-art performance in speech editing and very competitive results in zero-shot TTS, while not being explicitly trained on the latter task, outperforming leading autoregressive and diffusion models on diverse, real-world audio. By integrating Mamba for efficient audio sequence modeling with cross-attention for precise text-acoustic alignment, MAVE enables context-aware voice editing with exceptional naturalness and speaker consistency. In pairwise human evaluations on a random 40-sample subset of the RealEdit benchmark (400 judgments), 57.2% of listeners rated MAVE - edited speech as perceptually equal to the original, while 24.8% prefered the original and 18.0% MAVE - demonstrating that in the majority of cases edits are indistinguishable from the source. MAVE compares favorably with VoiceCraft and FluentSpeech both on pairwise comparisons and standalone mean opinion score (MOS) evaluations. For zero-shot TTS, MAVE exceeds VoiceCraft in both speaker similarity and naturalness, without requiring multiple inference runs or post-processing. Remarkably, these quality gains come with a significantly lower memory cost and approximately the same latency: MAVE requires ~6x less memory than VoiceCraft during inference on utterances from the RealEdit database (mean duration: 6.21s, A100, FP16, batch size 1). Our results demonstrate that MAVE establishes a new standard for flexible, high-fidelity voice editing and synthesis through the synergistic integration of structured state-space modeling and cross-modal attention.
COSPADI: Compressing LLMs via Calibration-Guided Sparse Dictionary Learning
Sep 26, 2025Abstract:Post-training compression of large language models (LLMs) largely relies on low-rank weight approximation, which represents each column of a weight matrix in a shared low-dimensional subspace. While this is a computationally efficient strategy, the imposed structural constraint is rigid and can lead to a noticeable model accuracy drop. In this work, we propose CoSpaDi (Compression via Sparse Dictionary Learning), a novel training-free compression framework that replaces low-rank decomposition with a more flexible structured sparse factorization in which each weight matrix is represented with a dense dictionary and a column-sparse coefficient matrix. This formulation enables a union-of-subspaces representation: different columns of the original weight matrix are approximated in distinct subspaces spanned by adaptively selected dictionary atoms, offering greater expressiveness than a single invariant basis. Crucially, CoSpaDi leverages a small calibration dataset to optimize the factorization such that the output activations of compressed projection layers closely match those of the original ones, thereby minimizing functional reconstruction error rather than mere weight approximation. This data-aware strategy preserves better model fidelity without any fine-tuning under reasonable compression ratios. Moreover, the resulting structured sparsity allows efficient sparse-dense matrix multiplication and is compatible with post-training quantization for further memory and latency gains. We evaluate CoSpaDi across multiple Llama and Qwen models under per-layer and per-group settings at 20-50\% compression ratios, demonstrating consistent superiority over state-of-the-art data-aware low-rank methods both in accuracy and perplexity. Our results establish structured sparse dictionary learning as a powerful alternative to conventional low-rank approaches for efficient LLM deployment.
Share Your Attention: Transformer Weight Sharing via Matrix-based Dictionary Learning
Aug 06, 2025Abstract:Large language models (LLMs) have revolutionized AI applications, yet their high computational and memory demands hinder their widespread deployment. Existing compression techniques focus on intra-block optimizations (e.g. low-rank approximation, attention head pruning), while the repetitive layered structure of transformers implies significant inter-block redundancy - a dimension largely unexplored beyond key-value (KV) caching. Inspired by dictionary learning in CNNs, we propose a framework for structured weight sharing across transformer layers. Our approach decomposes attention projection matrices into shared dictionary atoms, reducing the attention module's parameters by 66.7% while achieving on-par performance. Unlike complex methods requiring distillation or architectural changes, MASA (Matrix Atom Sharing in Attention) operates as a drop-in replacement - trained with standard optimizers - and represents each layer's weights as linear combinations of shared matrix atoms. Experiments across scales (100M-700M parameters) show that MASA achieves better benchmark accuracy and perplexity than grouped-query attention (GQA), low-rank baselines and recently proposed Repeat-all-over/Sequential sharing at comparable parameter budgets. Ablation studies confirm robustness to the dictionary size and the efficacy of shared representations in capturing cross-layer statistical regularities. Extending to Vision Transformers (ViT), MASA matches performance metrics on image classification and detection tasks with 66.7% fewer attention parameters. By combining dictionary learning strategies with transformer efficiency, MASA offers a scalable blueprint for parameter-efficient models without sacrificing performance. Finally, we investigate the possibility of employing MASA on pretrained LLMs to reduce their number of parameters without experiencing any significant drop in their performance.
ReplaceMe: Network Simplification via Layer Pruning and Linear Transformations
May 05, 2025Abstract:We introduce ReplaceMe, a generalized training-free depth pruning method that effectively replaces transformer blocks with a linear operation, while maintaining high performance for low compression ratios. In contrast to conventional pruning approaches that require additional training or fine-tuning, our approach requires only a small calibration dataset that is used to estimate a linear transformation to approximate the pruned blocks. This estimated linear mapping can be seamlessly merged with the remaining transformer blocks, eliminating the need for any additional network parameters. Our experiments show that ReplaceMe consistently outperforms other training-free approaches and remains highly competitive with state-of-the-art pruning methods that involve extensive retraining/fine-tuning and architectural modifications. Applied to several large language models (LLMs), ReplaceMe achieves up to 25% pruning while retaining approximately 90% of the original model's performance on open benchmarks - without any training or healing steps, resulting in minimal computational overhead (see Fig.1). We provide an open-source library implementing ReplaceMe alongside several state-of-the-art depth pruning techniques, available at this repository.
GSLoc: Visual Localization with 3D Gaussian Splatting
Oct 08, 2024

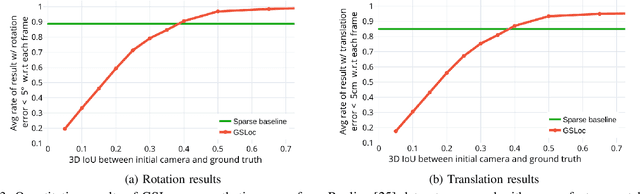
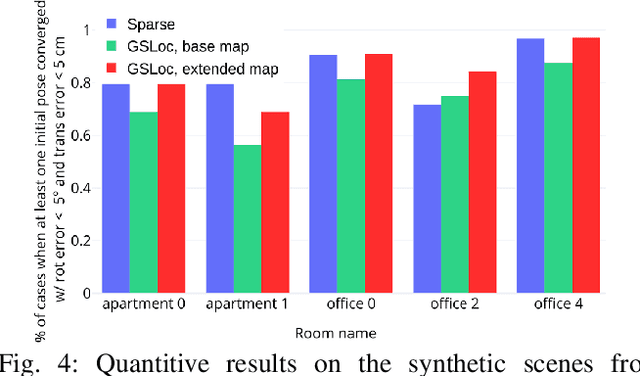
Abstract:We present GSLoc: a new visual localization method that performs dense camera alignment using 3D Gaussian Splatting as a map representation of the scene. GSLoc backpropagates pose gradients over the rendering pipeline to align the rendered and target images, while it adopts a coarse-to-fine strategy by utilizing blurring kernels to mitigate the non-convexity of the problem and improve the convergence. The results show that our approach succeeds at visual localization in challenging conditions of relatively small overlap between initial and target frames inside textureless environments when state-of-the-art neural sparse methods provide inferior results. Using the byproduct of realistic rendering from the 3DGS map representation, we show how to enhance localization results by mixing a set of observed and virtual reference keyframes when solving the image retrieval problem. We evaluate our method both on synthetic and real-world data, discussing its advantages and application potential.
NeuSD: Surface Completion with Multi-View Text-to-Image Diffusion
Dec 07, 2023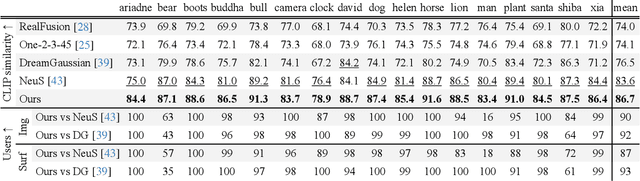


Abstract:We present a novel method for 3D surface reconstruction from multiple images where only a part of the object of interest is captured. Our approach builds on two recent developments: surface reconstruction using neural radiance fields for the reconstruction of the visible parts of the surface, and guidance of pre-trained 2D diffusion models in the form of Score Distillation Sampling (SDS) to complete the shape in unobserved regions in a plausible manner. We introduce three components. First, we suggest employing normal maps as a pure geometric representation for SDS instead of color renderings which are entangled with the appearance information. Second, we introduce the freezing of the SDS noise during training which results in more coherent gradients and better convergence. Third, we propose Multi-View SDS as a way to condition the generation of the non-observable part of the surface without fine-tuning or making changes to the underlying 2D Stable Diffusion model. We evaluate our approach on the BlendedMVS dataset demonstrating significant qualitative and quantitative improvements over competing methods.
Iterative Reweighted Least Squares Networks With Convergence Guarantees for Solving Inverse Imaging Problems
Aug 10, 2023



Abstract:In this work we present a novel optimization strategy for image reconstruction tasks under analysis-based image regularization, which promotes sparse and/or low-rank solutions in some learned transform domain. We parameterize such regularizers using potential functions that correspond to weighted extensions of the $\ell_p^p$-vector and $\mathcal{S}_p^p$ Schatten-matrix quasi-norms with $0 < p \le 1$. Our proposed minimization strategy extends the Iteratively Reweighted Least Squares (IRLS) method, typically used for synthesis-based $\ell_p$ and $\mathcal{S}_p$ norm and analysis-based $\ell_1$ and nuclear norm regularization. We prove that under mild conditions our minimization algorithm converges linearly to a stationary point, and we provide an upper bound for its convergence rate. Further, to select the parameters of the regularizers that deliver the best results for the problem at hand, we propose to learn them from training data by formulating the supervised learning process as a stochastic bilevel optimization problem. We show that thanks to the convergence guarantees of our proposed minimization strategy, such optimization can be successfully performed with a memory-efficient implicit back-propagation scheme. We implement our learned IRLS variants as recurrent networks and assess their performance on the challenging image reconstruction tasks of non-blind deblurring, super-resolution and demosaicking. The comparisons against other existing learned reconstruction approaches demonstrate that our overall method is very competitive and in many cases outperforms existing unrolled networks, whose number of parameters is orders of magnitude higher than in our case.
Learning Sparse and Low-Rank Priors for Image Recovery via Iterative Reweighted Least Squares Minimization
Apr 20, 2023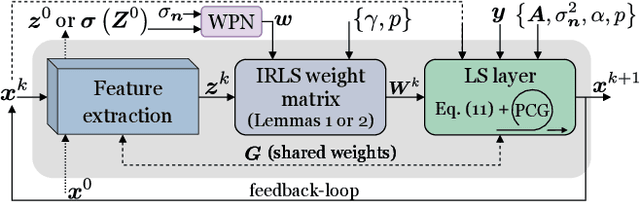


Abstract:We introduce a novel optimization algorithm for image recovery under learned sparse and low-rank constraints, which we parameterize as weighted extensions of the $\ell_p^p$-vector and $\mathcal S_p^p$ Schatten-matrix quasi-norms for $0\!<p\!\le1$, respectively. Our proposed algorithm generalizes the Iteratively Reweighted Least Squares (IRLS) method, used for signal recovery under $\ell_1$ and nuclear-norm constrained minimization. Further, we interpret our overall minimization approach as a recurrent network that we then employ to deal with inverse low-level computer vision problems. Thanks to the convergence guarantees that our IRLS strategy offers, we are able to train the derived reconstruction networks using a memory-efficient implicit back-propagation scheme, which does not pose any restrictions on their effective depth. To assess our networks' performance, we compare them against other existing reconstruction methods on several inverse problems, namely image deblurring, super-resolution, demosaicking and sparse recovery. Our reconstruction results are shown to be very competitive and in many cases outperform those of existing unrolled networks, whose number of parameters is orders of magnitude higher than that of our learned models.
DeepRLS: A Recurrent Network Architecture with Least Squares Implicit Layers for Non-blind Image Deconvolution
Dec 10, 2021
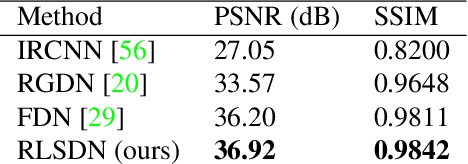
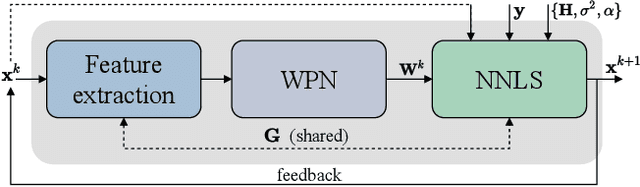
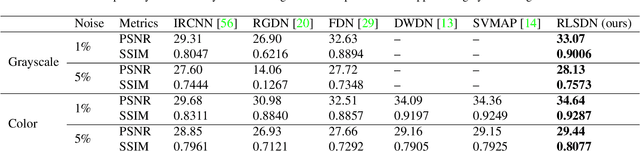
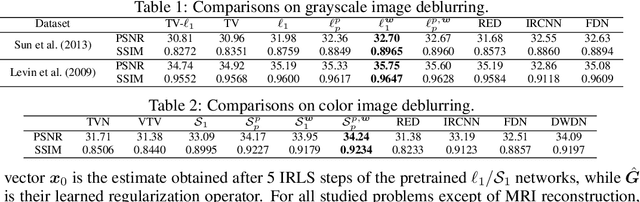
Abstract:In this work, we study the problem of non-blind image deconvolution and propose a novel recurrent network architecture that leads to very competitive restoration results of high image quality. Motivated by the computational efficiency and robustness of existing large scale linear solvers, we manage to express the solution to this problem as the solution of a series of adaptive non-negative least-squares problems. This gives rise to our proposed Recurrent Least Squares Deconvolution Network (RLSDN) architecture, which consists of an implicit layer that imposes a linear constraint between its input and output. By design, our network manages to serve two important purposes simultaneously. The first is that it implicitly models an effective image prior that can adequately characterize the set of natural images, while the second is that it recovers the corresponding maximum a posteriori (MAP) estimate. Experiments on publicly available datasets, comparing recent state-of-the-art methods, show that our proposed RLSDN approach achieves the best reported performance both for grayscale and color images for all tested scenarios. Furthermore, we introduce a novel training strategy that can be adopted by any network architecture that involves the solution of linear systems as part of its pipeline. Our strategy eliminates completely the need to unroll the iterations required by the linear solver and, thus, it reduces significantly the memory footprint during training. Consequently, this enables the training of deeper network architectures which can further improve the reconstruction results.
Microscopy Image Restoration with Deep Wiener-Kolmogorov filters
Dec 25, 2019



Abstract:Microscopy is a powerful visualization tool in biology, enabling the study of cells, tissues, and the fundamental biological processes. Yet, the observed images of the objects at the micro-scale suffer from two major inherent distortions: the blur caused by the diffraction of light, and the background noise caused by the imperfections of the imaging detectors. The latter is especially severe in fluorescence and in confocal microscopes, which are known for operating at the low photon count with the Poisson noise statistics. Restoration of such images is usually accomplished by image deconvolution, with the nature of the noise statistics taken into account, and by solving an optimization problem given some prior information about the underlying data (i.e., regularization). In this work, we propose a unifying framework of algorithms for Poisson image deblurring and denoising. The algorithms are based on deep learning techniques for the design of learnable regularizers paired with an appropriate optimization scheme. Our extensive experimentation line showcases that the proposed approach achieves superior quality of image reconstruction and beats the solutions that rely on deep learning or on the optimization schemes alone. Moreover, several implementations of the proposed framework demonstrate competitive performance at a low computational complexity, which is of high importance for real-time imaging applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge